Fractales de Newton

IRecherche des zéros d'une fonction

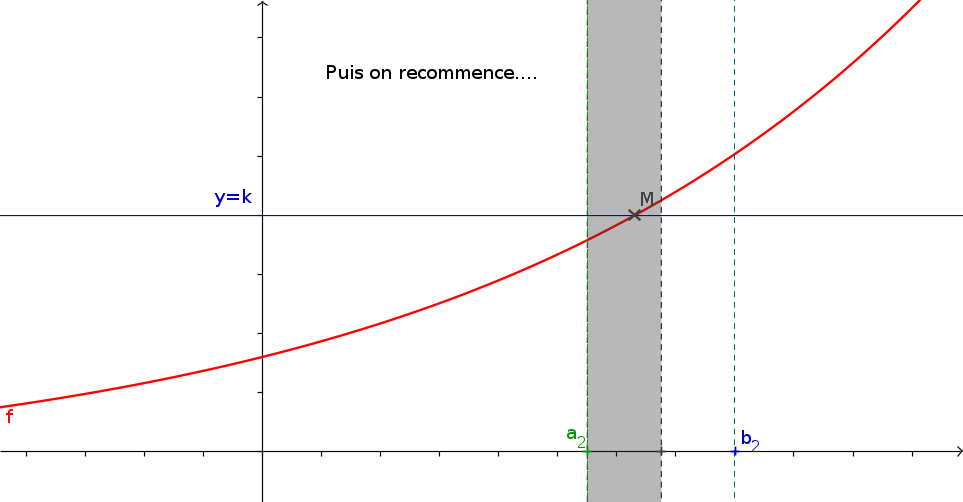
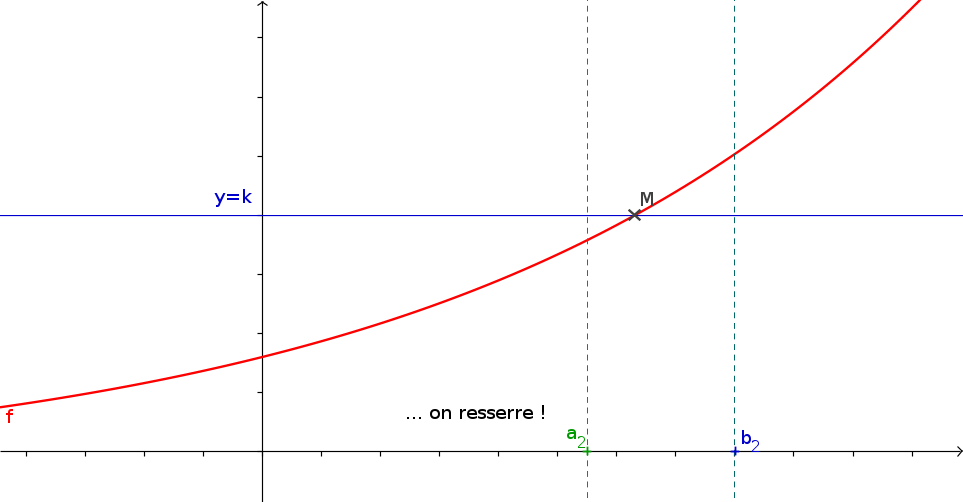
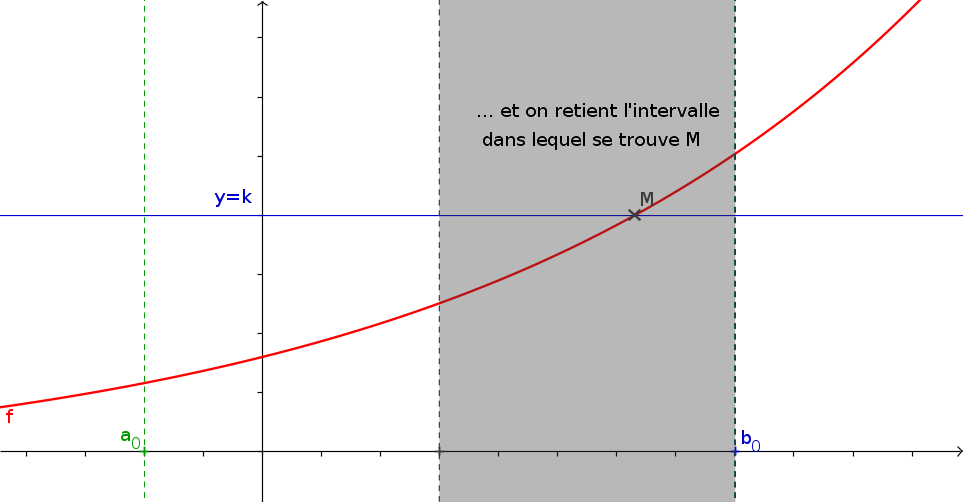
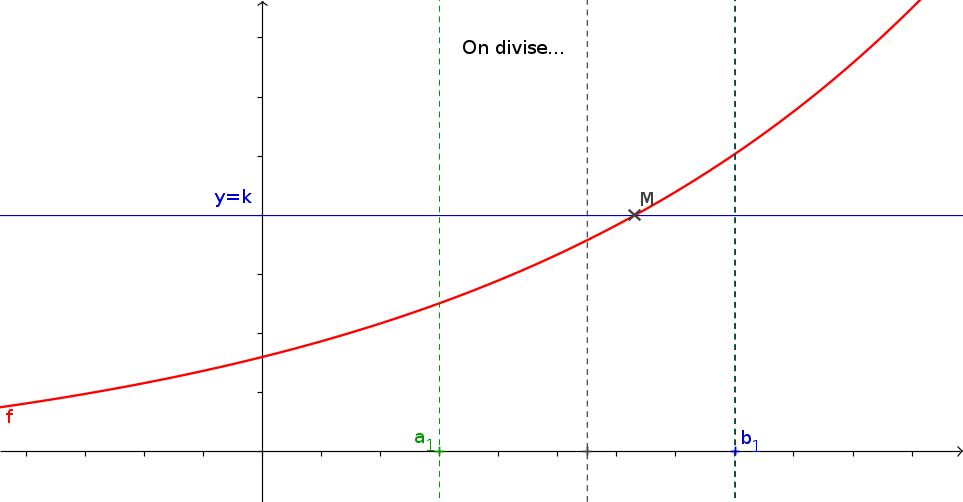
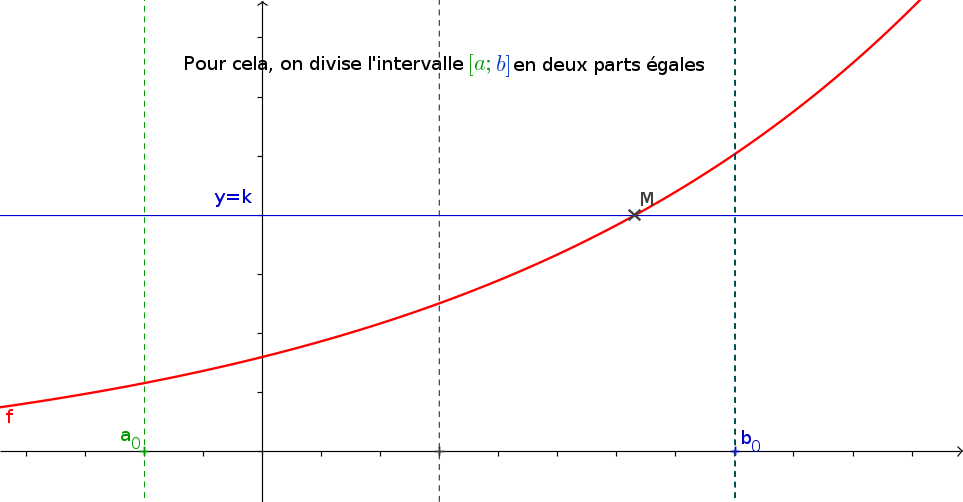
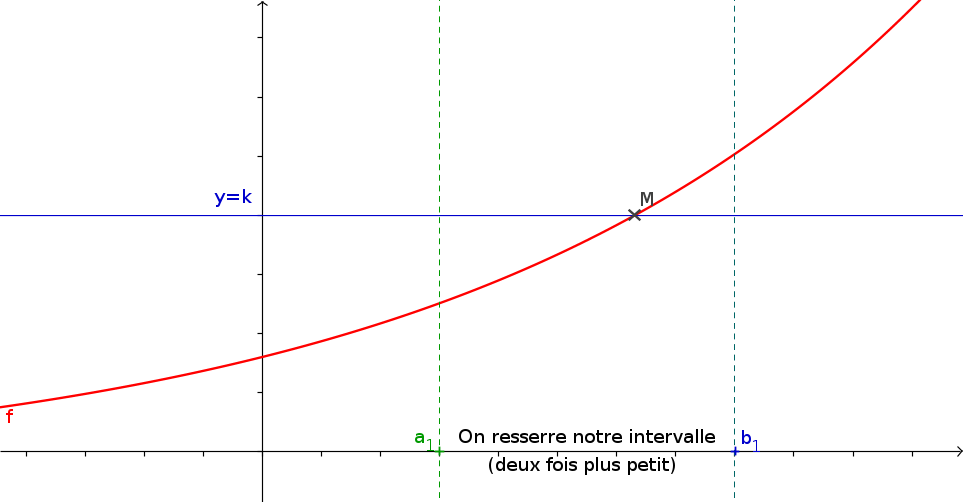
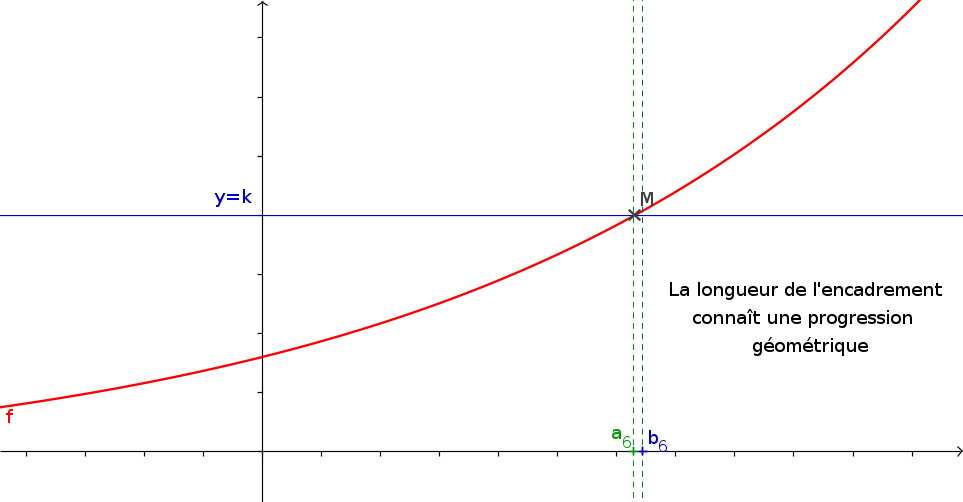
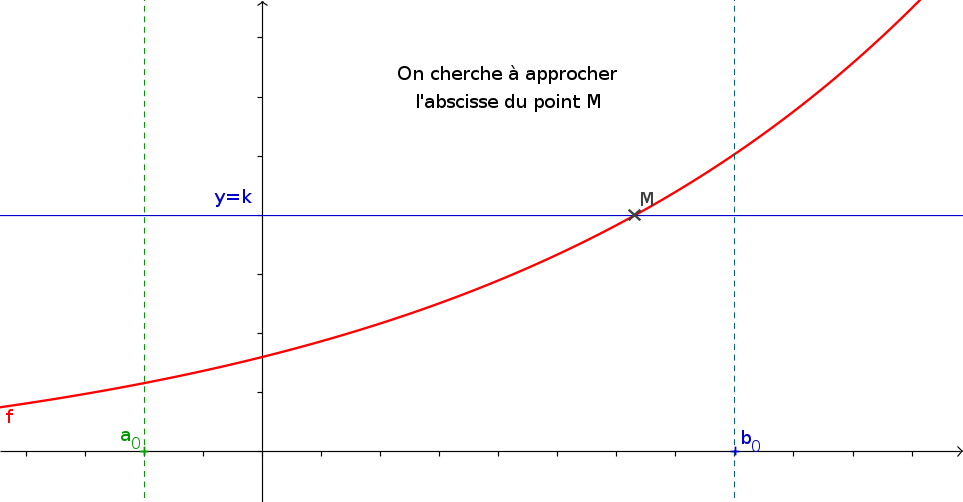
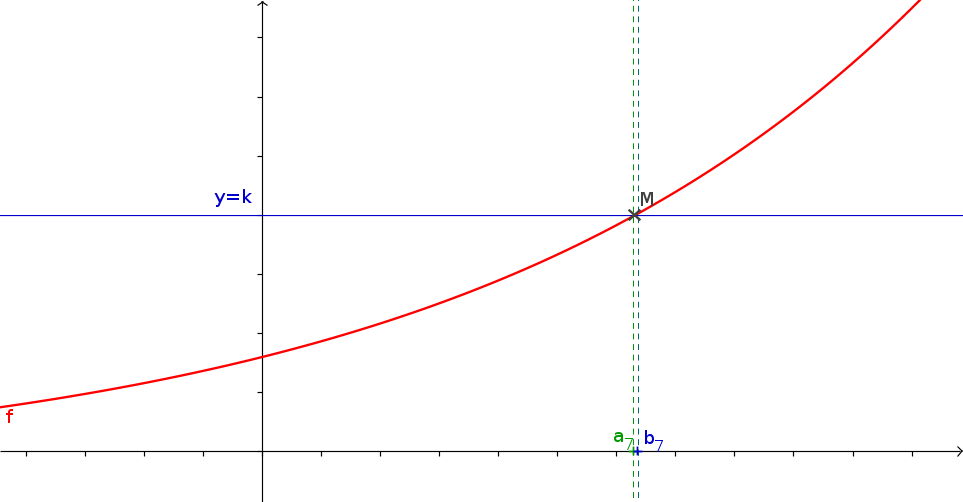
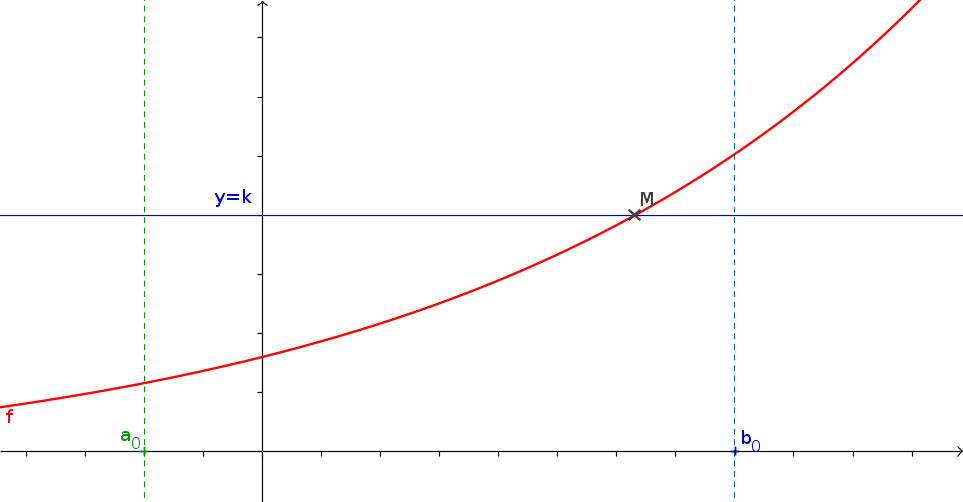
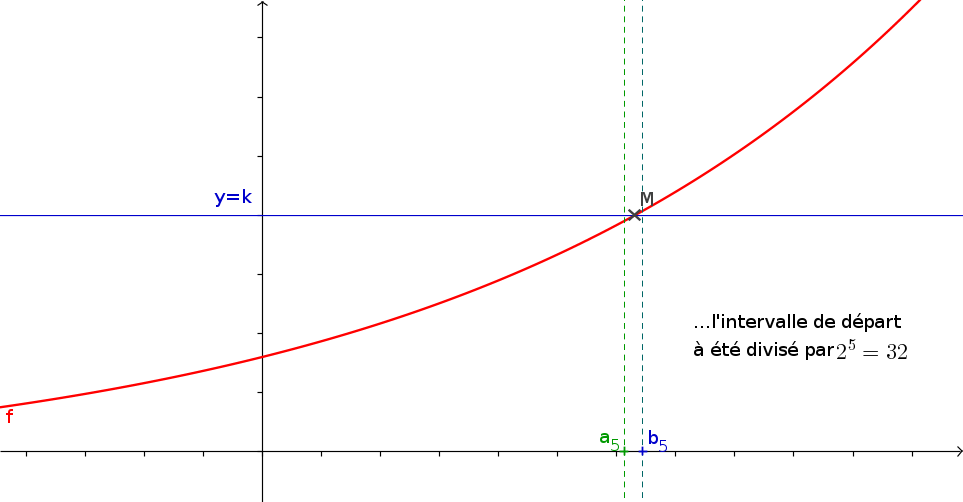
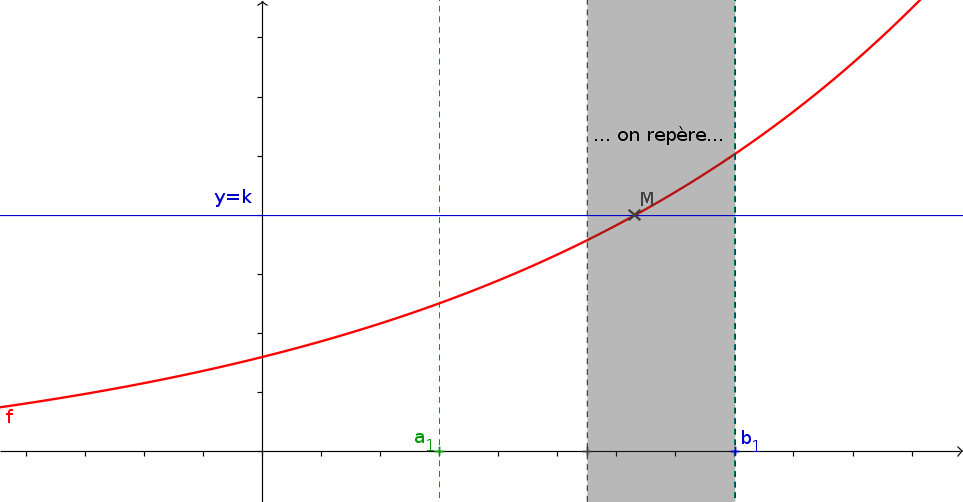
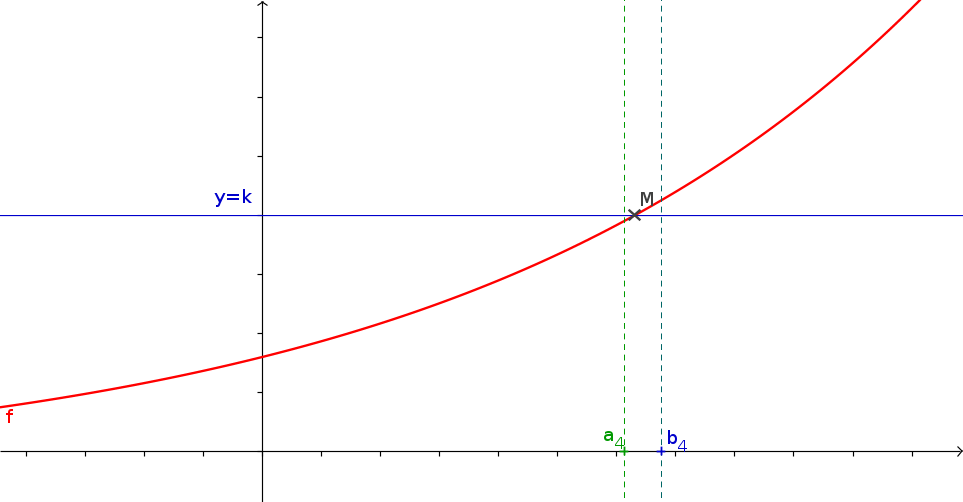
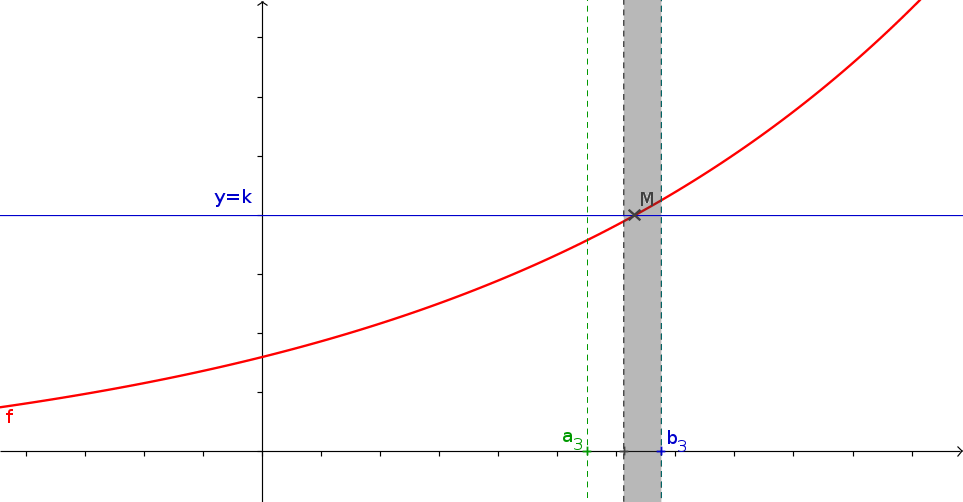
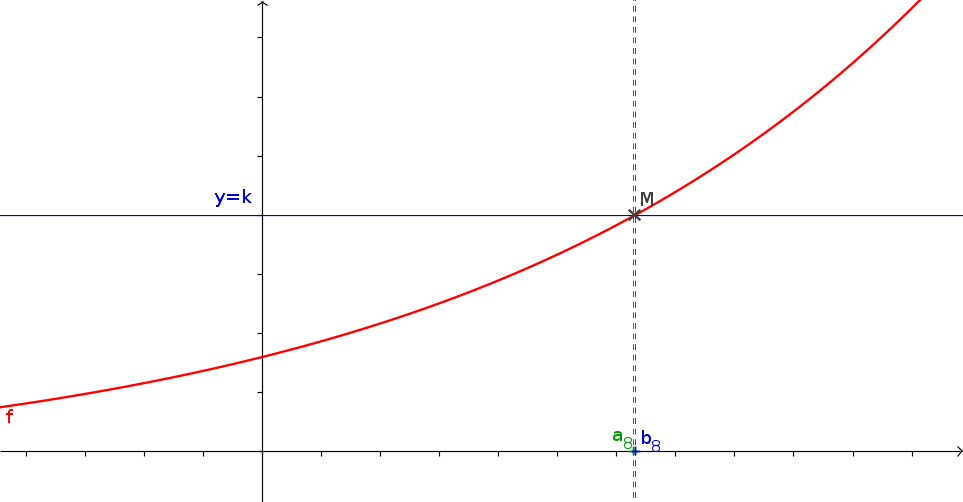
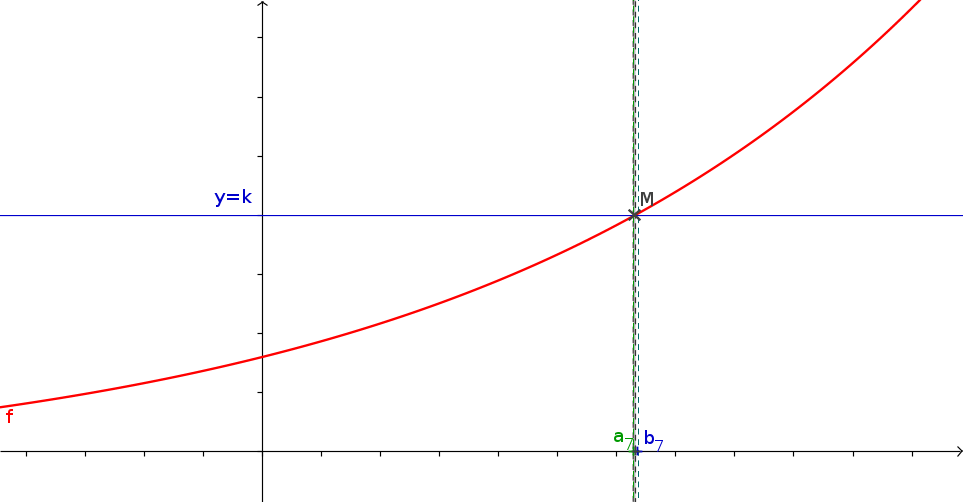
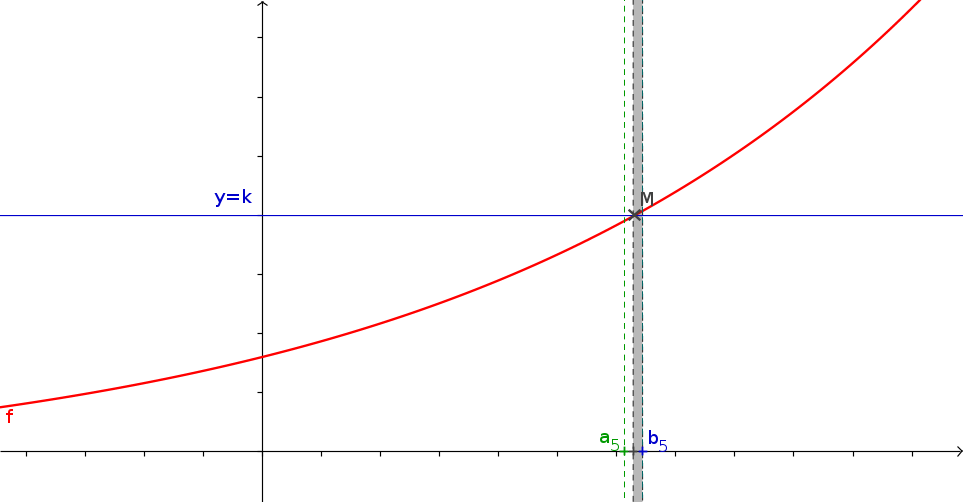
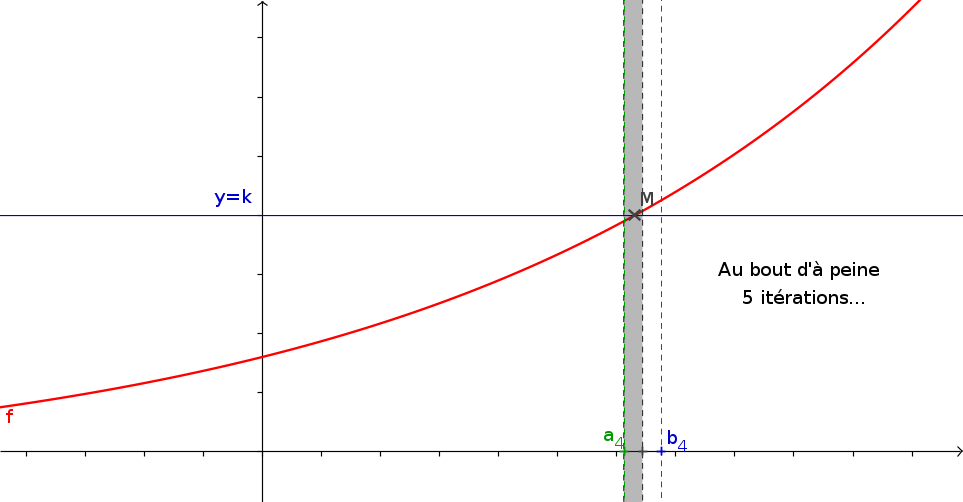
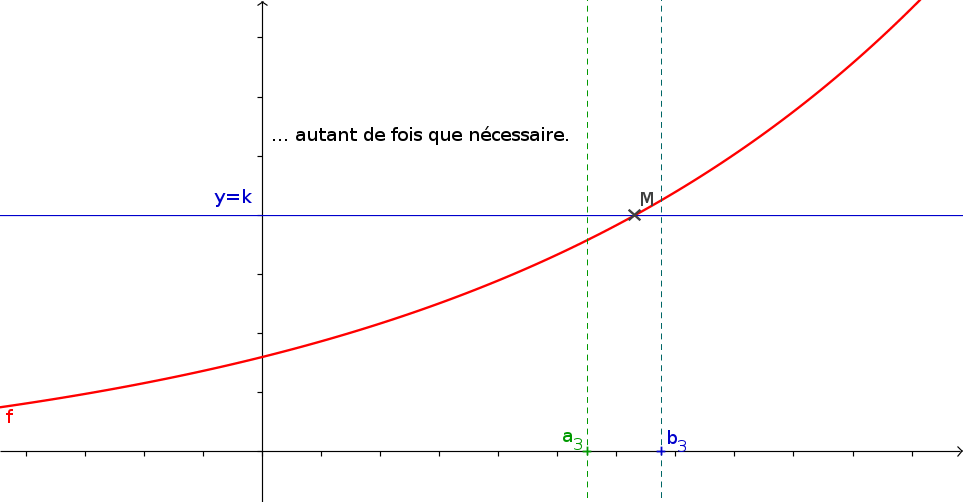
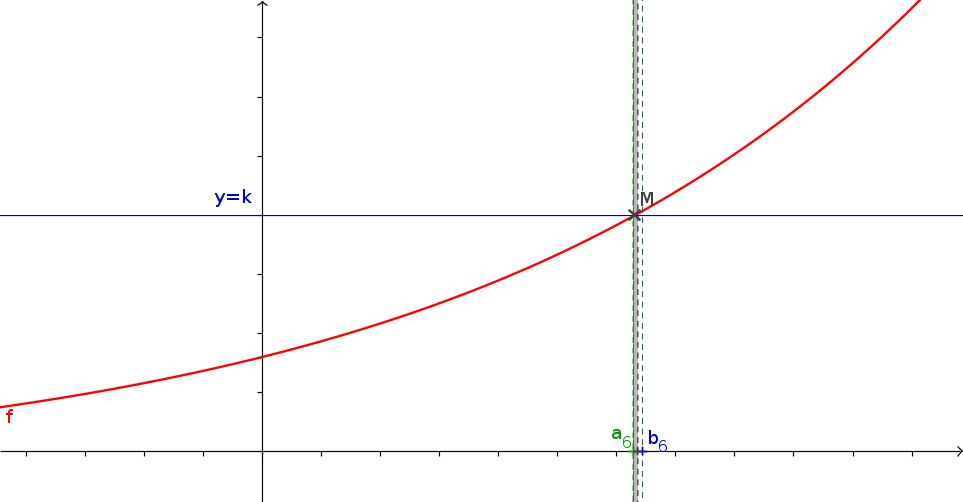
On s'intéresse à une fonction $f: \mathbb{R} \rightarrow \mathbb{R} $ continue s'annulant une seule fois en $\xi$ sur $[a,b]$

1La méthode de la dichotomie

L'animation ci-dessous rappelle le fonctionnement général de l'algorithme de dichotomie pour une fonction croissante (cas général $f (x) = k$) :

Programmer une fonction dichotomie(f,a,b,p) où :

f est une fonction continue s'annulant une unique fois sur $[a;b]$ que vous aurez créé.
a et b les bornes de l'intervalle
p (un flottant) la précision de l'approximation souhaitée

Utiliser la méthode de la dichotomie pour approximer $\pi$, à l'aide d'une fonction que vous aurez choisie.

2La méthode de Newton

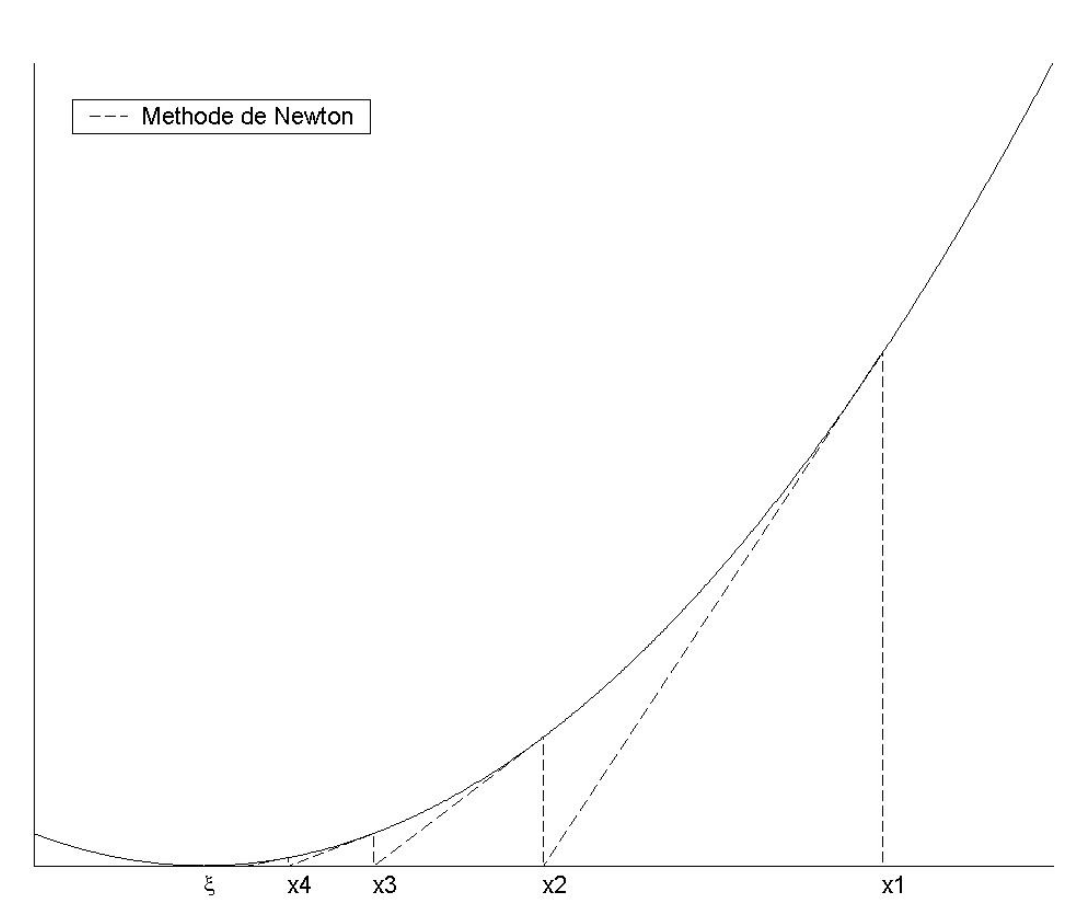
La méthode de Newton est une autre méthode d'approximation très rapide des zéros de $f$ mais nécessitant la dérivée de la fonction. Nous l'appliquerons ici à un polynôme $f: \mathbb{C} \rightarrow \mathbb{C} $ et noterons $f'$ sont polynôme dérivé.

On construit de même une suite qui converge vers $\xi$ de la manière suivante:

On choisit pour $x_{0}$ un point proche de $\xi$. Le n-ème point est obtenu comme le point d'intersection entre l'axe des abscisses et la tangente à la courbe en $(x_{n-1},f(x_{n-1}))$. La suite s'itère de la manière suivante : $$ \left \{ \begin{array}{l} x_0 \text{ proche de }\xi \\ x_{n+1}= x_n - \frac{f(x_n)}{f'(x_n)} \\ \end{array} \right. $$ En s'assurant que $f'(x_0), f'(x_1),...$ sont non nuls.

Programmer une fonction newton(f,fp,p) où :

f est un polynôme.
fp est le polynôme dérivé
p (un flottant) la précision de l'approximation souhaitée

Cette fonction doit renvoyer un nombre complexe (ou réel) qui correspond au premier élément de la suite qui est à distance $p$ de son prédécesseur.

Vérifier que la méthode fonctionne pour approximer le nombre d'or.

Il est possible d'améliorer la fonction en créant deux fonctions polynome(L) et derivee_poly(L) pour éviter d'avoir à calculer la dérivée soi-même et faire fonctionner la méthode de Newton sur des polynômes.

IIL'ensemble de Mandelbrot

L'ensemble de Mandelbrot est une fractale qui est définie comme l'ensemble des points c du plan complexe pour lesquels la suite récurrente définie par : $$ \left \{ \begin{array}{l} z_0 = 0 \\ z_{n+1}=z_n^2 + c \\ \end{array} \right. $$ ne tend pas vers l'infini en module.

Programmer une fonction suite_mandel(z0,n) où :

z0 est le terme unitial.
n l'indice du terme à renvoyer

La fonction doit renvoyer le $n$-ième terme de la suite définie avant.

Il peut être démontré que dès que le module de $z_n$ est strictement plus grand que 2, la suite diverge vers l'infini, et donc $c$ est en dehors de l'ensemble de Mandelbrot.

Programmer une fonction converge_mandel(z0) où z0 est le terme initial de la suite. On considèrera que la suite diverge si $|z_{30}| \lt 2$.

Cette propriété nous permet d'arrêter le calcul pour les points ayant un module strictement supérieur à 2 et qui sont donc en dehors de l'ensemble de Mandelbrot. Pour les points de l'ensemble de Mandelbrot, i.e. les nombres complexes $c$ pour lesquels $z_n$ ne tend pas vers l'infini, le calcul n'arrivera jamais à terme, donc il doit être arrêté après un certain nombre d'itérations déterminé par le programme. Il en résulte que l'image affichée n'est qu'une approximation du vrai ensemble.

Programmer une fonction mandelbrot(xmin,xmax,ymin,ymax,p) où :

xmin , xmax , ymin , ymax sont les bords de la zone affichée
p est la précision affichée (plus petit il sera plus précise sera la figure)

Pour dessiner l'ensemble de Mandelbrot :

On fera varier $c$ dans le rectangle avec $Re(c) \in [xmin,xmax]$ et $Im(c) \in [ymin,ymax]$
On trace le point si la suite "converge" (au sens de notre fonction précédente)

Pour afficher l'ensemble de Mandelbrot en entier, choisir : $Re(c) \in [-2,1]$ et $Im(c) \in [-1,1]$.

Cliquer pour voir des indices

Replier

La zone affichées soit être subdivisée en carrés de largeur $p$.
Plutôt que de tracer des simples points, il serait préférable de tracer des Rectangle pleins.
Afin de parcourir les points du plan, il faudra faire une double boucle :
for i in range(0,N):
for j in range(0,M):
...
$N = \frac{xmax-xmin}{p}$ et $M = \frac{ymax-ymin}{p}$
Pour tous i et j de la boucle, tracer rect=plt.Rectangle((xmin+i*p, ymin+j*p), p, p)

IIIFractale de Newton

La méthode de Newton peut-être très efficace pour estimer les racines d'une fonction d'une façon très précise en quelques parfois étapes seulement. Lorsqu'on utilise une valeur initiale suffisamment près d'une racine, la méthode de Newton converge en général très rapidement vers cette racine. Ce n'est pourtant pas une condition nécessaire, et les fractales de Newton représentent cette répartition des valeurs initiales en fonction du déroulement de la méthode.

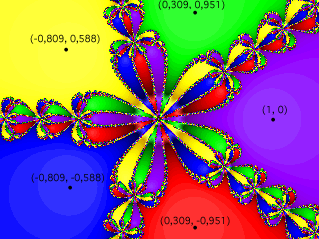
Prenons comme exemple, le polynôme $X^5 - 1$. Il possède 5 racines complexes : $1; e^{\frac{2i \pi}{5}}; e^{\frac{4i \pi}{5}}; e^{\frac{6i \pi}{5}}; e^{\frac{8i \pi}{5}} $. On peut observer sur la figure ci-dessous les cinq zones de convergence de la méthode vers les cinq racines :

Programmer une fonction fractale_newton(xmin,xmax,ymin,ymax,f,fp,p) où :

xmin , xmax , ymin , ymax sont les bords de la zone affichée
p est la précision affichée (plus petit il sera plus précise sera la figure)
f est le polynôme
fp est la dérivée du polynôme

Pour dessiner la fractale de Newton associé au polynôme f :

On fera varier $c$ dans le rectangle avec $Re(c) \in [xmin,xmax]$ et $Im(c) \in [ymin,ymax]$
On trace le point si la méthode de Newton "converge" (tester 10 itérations)

Cliquer pour voir des indices

Replier

Le principe est le même que dans l'ensemble de Mandelbrot. Cette fois, on fera varier le premier terme $z_0$ dans un rectangle suffisamment large et on le tracera lorsque la méthode de Newton converge (on itèrera les 10 premiers termes de la suite).

Pour aller plus loin :

Tester avec d'autre polynômes
Ajouter une coloration selon la racine vers laquelle la méthode converge
Faire un dégrader de couleur lié à la distance de divegence mesurée