Warning: call_user_func_array() expects parameter 1 to be a valid callback, class 'cMath' does not have a method 'f' in /volume1/web/lycee/fonctions/fonctions.php on line 163 Call Stack: 0.0002 352480 1. {main}() /volume1/web/lycee/ressources_scolaires/TS/01 - Derivation/Cours/Dérivation.php:0 0.0006 353296 2. cMath->add() /volume1/web/lycee/ressources_scolaires/TS/01 - Derivation/Cours/Dérivation.php:30 0.0072 365616 3. cMath->commands() /volume1/web/lycee/fonctions/fonctions.php:113 0.0327 408720 4. cMath->commands() /volume1/web/lycee/fonctions/fonctions.php:158 0.0339 409720 5. cMath->commands() /volume1/web/lycee/fonctions/fonctions.php:245

Chapitre 1 - Dérivation

Connaître les dérivées usuelles
Calculer l'équation de la tangente à un point
Etudier les variations d'une fonction à l'aide de sa dérivée
Calculer les dérivées des fonctions $x \mapsto \sqrt{u (x)}$, $x \mapsto (u (x))^n$
Calculer la dérivées d'une fonction $x \mapsto f (a x+b)$

IRappels sur le nombre dérivé

Le nombre dérivé a une interprétation géométrique :

Le nombre dérivée $f '(a)$ est le coefficient directeur de la droite tangente (si elle existe) à la courbe en $x=a$.

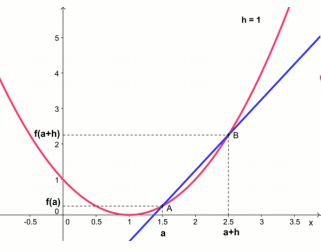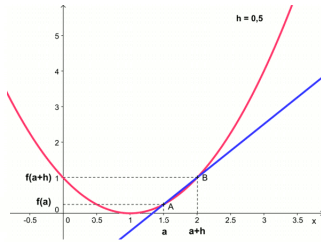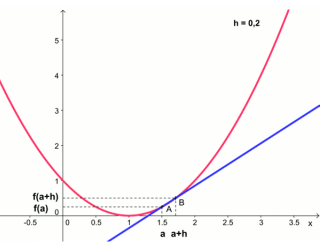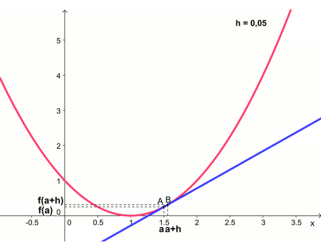
$tangente en $a$$

Toutes les fonctions n'admettent pas forcément des tangentes partout, comme on peut le voir sur les exemples suivants :

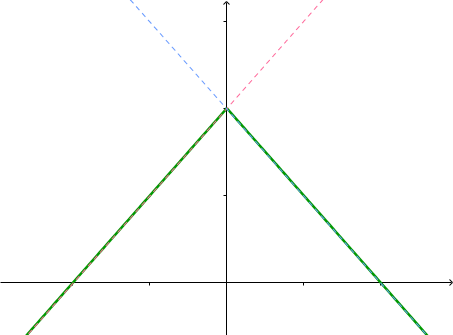En $x=0$, on ne peut pas définir une tangente unique. La fonction n'est pas dérivable en 0

La fonction $x\longmapsto \sqrt{x}$ n'est pas dérivable en $0$ :

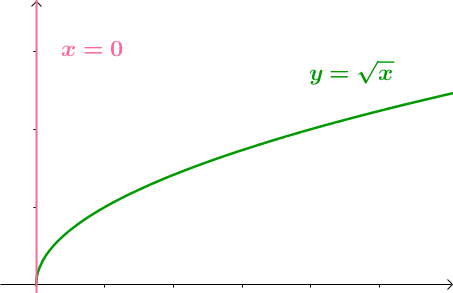En $x=0$, la tangente est verticale. Une droite verticale n'a pas de coefficient directeur, donc pas de nombre dérivé.

Le coefficient directeur de la droite passant par les points $A (x_A;y_A)$ et $B (x_B;y_B)$ s'obtient en calculant le taux d'accroissement : $$\frac{y_B - y_A}{x_B - x_A}$$

Sur la courbe précédente, le coefficient directeur de la droite passant par $ A (a,f (a))$ et $M (a+h, f (a+h))$ vaut :

Cliquer pour dévoiler

Replier

$$\frac{f (a+h) - f (a)}{x+h - x} = \frac{f (a+h) - f (a)}{h}$$

La véritable définition reprend cette idée de "rapprocher" les points $A$ et $M$ en diminuant $h$. Autrement dit, en faisant tendre $h$ vers 0 :

Soit une fonction $f$ définie sur un intervalle $I$ et $a \in I$.

La fonction $f$ est dérivable en $a$ si le taux d'accroissement $\frac{f (a+h) - f (a)}{h}$ admet une limite finie quand $h$ tend vers $0$.

Ce que l'on note : $f'(a)=\lim\limits_{h \rightarrow 0} \frac{f (a+h) -}{h}$

Dans ce cas, on appelle nombre dérivé en $a$ cette limite notée $f'(a)$

IIRappels : propriétés de la fonction dérivée

AFonctions usuelles

On note $f'$ la fonction dérivée associée à la fonction $f$ :

$$ \begin{array}{|c|c|c|c|} \hline f & f' & f \text{ définie sur} \\\hline k \text{ (constante)} & 0 & \mathbb{R} \\\hline x & 1 & \mathbb{R} \\\hline x^2 & x & \mathbb{R} \\\hline x^3 & 3x^{2} & \mathbb{R} \\ \hline x^n & nx^{n-1} & \mathbb{R} \text{ où }(n\geq 0) \\ \hline\hline \frac{1}{x} &\frac{-1}{x^2} & ]0;+\infty[ \text{ ou } ]\infty;0[ \\\hline \frac{1}{x^n} & \frac{-n}{x^{n+1}} & ]0;+\infty[ \text{ ou } ]\infty;0[ \text{ où }(n\geq 0) \\ \hline\hline \sqrt{x} & \frac{1}{2\sqrt{x}} & \begin{array}{cc} f \text{définie sur }[0;+\infty[\\ \text{et dérivable sur }]0;+\infty[\end{array} \\\hline cos (x) & -sin (x) & \mathbb{R} \\\hline sin (x) & cos (x) & \mathbb{R} \\\hline \end{array} $$

BEtude de signe

La signe de la fonction dérivée nous permet de déduire les variations de la fonction de départ :

$f$ est dérivable, définie sur un intervalle $I$ :

Si $f'$ est positive sur $I$, alors $f$ est croissante sur $I$
Si $f'$ est négative sur $I$, alors $f$ est décroissante sur $I$
Si $f'$ est nulle sur $I$, alors $f$ est constante sur $I$

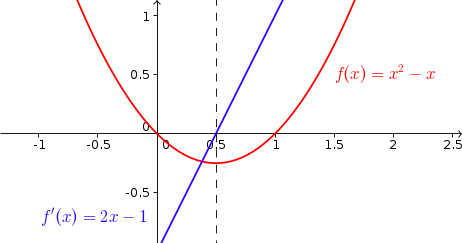On trace la fonction d'équation $f (x) = x^2 - x$ et sa dérivée $f'(x) = 2 x - 1$ :

On observe en effet que :

Pour $x \lt 0,5$, $f'(x) \lt 0$ et $f$ est décroissante
Pour $x \gt 0,5$, $f'(x) \gt 0$ et $f$ est croissante

Ce que l'on peut résumer par les tableaux suivant : $$ \begin{array}{c|lcccr|} x &-\infty & & 0,5 & & +\infty\\\hline f' (x) & & - & 0 & + & \\ \hline f (x) & & \searrow & f (0,5) & \nearrow & \\ \end{array} $$ La première ligne décrit l'axe des abscisses. La deuxième ligne donne le signe de la dérivée $f'$. La troisième ligne donne les variations de la fonction $f$.

La fonction précédente est un exemple (trop) simple qui peut être traité plus simplement à l'aide des connaissances de première sur les polynômes du second degré.

CEquation de la tangente

Soit une fonction $f$ définie sur un intervalle $I$ et $a \in I$.

L'équation de la tangente à la courbe $C_f$ en $x=a$, notée $T_a$ est : $$ T_a : y=f'(a) (x-a) + f (a)$$

Nous souhaitons tracer la tangente de l'hyperbole d'équation $f (x) = \frac{1}{x}$ en $x=1$. Pour cela il va falloir passer par un calcul de dérivée et utiliser la propriété précédente :

$f'(x)=\frac{-1}{x^2}$, donc $f'(1) = -1$. De plus, $f (1) = 1$.

L'équation de la tangente en $x=1$ est : $$ \begin{array}{lll} T_1 : y&=&f'(1) (x-1) + f (1)\\ &=&-1\times (x-1) + 1 \\ T_1 : y&=&-x+2 \end{array} $$ Il n'y a plus qu'à représenter graphiquement :

IIIOpérations sur les fonctions dérivables

Soient $u$ et $v$ deux fonctions dérivables sur un intervalle $I$ et $k$ un nombre réel.

Alors les fonctions $u+v$, $ku$, $uv$ sont dérivables sur $I$ et $\frac{u}{v}$ aussi si $v$ ne s'annule pas :

$(u+v)'=u' + v'$
$(u-v)'=u' - v'$
$(k u)'=k u'$
$(u v)'=u' v + u v'$
$(\frac{u}{v})'=\frac{u' v - u v'}{v^2}$

Soit $n$ un entier et $u$ une fonction dérivable sur $I$.

Alors la fonction $x \mapsto u (x)^n$ (notée $u^n$) est dérivable sur $I$ et : $$(u^n)' = n u' u^{n-1}$$

On reprend les mêmes notations et on suppose que $u (x) \neq 0$ sur $I$

Alors la fonction $x \mapsto \frac{1}{u (x)^n}$ (notée $\frac{1}{u^n}$ ou $u^{-n}$) est dérivable sur $I$ et : $$(\frac{1}{u^n})' = -n \frac{u'}{u^{n+1}} = -n u' u^{-n-1}$$

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f (x)= (x-1)^3$.

Nous sommes dans le cas de propriété précédente avec $u= (x-1)$ et $n=3$. On a $u' = 1$ et donc :

$$ \begin{array}{lll} f'(x)&=&3 \times 1 \times (x-1)^{3-1}\\ &=&3 (x-1)^{2}\\ \end{array} $$

Soit $u$ une fonction dérivable sur $I$ telle que $u (x) \gt 0$.

Alors la fonction $x \mapsto \sqrt{u (x)}$ (notée $\sqrt{u}$) est dérivable sur $I$ et : $$(\sqrt{u})' = \frac{u'}{2 \sqrt{u}}$$

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f (x)= \sqrt{3 x+2}$.

Nous sommes dans le cas de propriété précédente avec $u= (4x+2)$. On a $u' = 3$ et donc :

$$ \begin{array}{lll} f'(x)&=&\frac{4}{2 \sqrt{3x+2}}\\ &=&\frac{2}{\sqrt{3x+1}}\\ \end{array} $$

Soient $I$,$J$ deux intervalles, $v$ une fonction de $I$ dans $J$, et $u$ une fonction definie sur $J$

On suppose que les deux fonctions sont dérivables.

Soit $f (x) = u (v (x))$ la fonction composée, définie sur $I$

Alors la fonction $f$ est dérivable sur $I$ et : $$f'(x) = v'(x) u' (v (x))$$

On peut en déduire la propriété suivante :

Soient $a, b \in \mathbb{R}$. On pose $f (x) = cos (a x + b)$ et $g (x) = sin (a x + b)$. Alors, $f$ et $g$ sont dérivables et :

$$ f' (x) = - a \text{ } sin (a x + b) $$ $$ g'(x) = a \text{ } cos (a x+b) $$

Cliquer pour dévoiler

Replier

Pour $f (x) = cos (a x + b)$, on applique la propriété avec $v (x) = a x + b$, $u (x) = cos (x)$, $v'(x) = a$ et $u'(x)=-sin (x)$.

Et donc :

$$ \begin{array}{lll} f'(x)&=& v'(x) u' (v (x))\\ &=&a \times (- sin (a x + b) )\\ &=&- a \text{ } sin (a x + b)\\ \end{array} $$

On raisonne de même pour $g (x) = sin (a x + b)$, avec $v (x) = a x + b$, $u (x) = sin (x)$, $v'(x) = a$ et $u'(x)=cos (x)$.

Et donc :

$$ \begin{array}{lll} f'(x)&=& v'(x) u' (v (x))\\ &=&a \text{ } cos (a x + b)\\ \end{array} $$

Les formules de $(u^n)'$, $\sqrt{u}'$ et $(\frac{1}{u^n})'$ peuvent se retrouver de la même manière avec cette propriété sur les fonctions composées. v'(x) u' (v (x))