Chapitre 11 - Formes trigonométrique et algébrique des nombres complexes
- Forme trigonométrique : module et argument, interprétation géométrique
- Notation exponentielle
- Passer de la forme algébrique à la forme trigonométrique et inversement
- Connaître et utiliser la relation \(z\bar{z} = |z|^2\)
- Effectuer des opérations sur les nombres complexes écrits sous différentes formes
IForme trigonométrique
1Introduction
En revenant à l'interprétation géométrique d'un nombre complexe \(z=a + i b\), c'est à dire un point \(M (a;b)\) dans le plan, puis en utilisant le cercle trigonométrique pour le repérer, on peut écrire \(z\) sous une forme nouvelle, la forme trigonométrique...
On se place dans le plan muni d'un repère orthonormé \((O;\vec{u};\vec{v})\) et on place \(M\) le point d'affixe \(z=a+ib\) un nombre complexe non nul.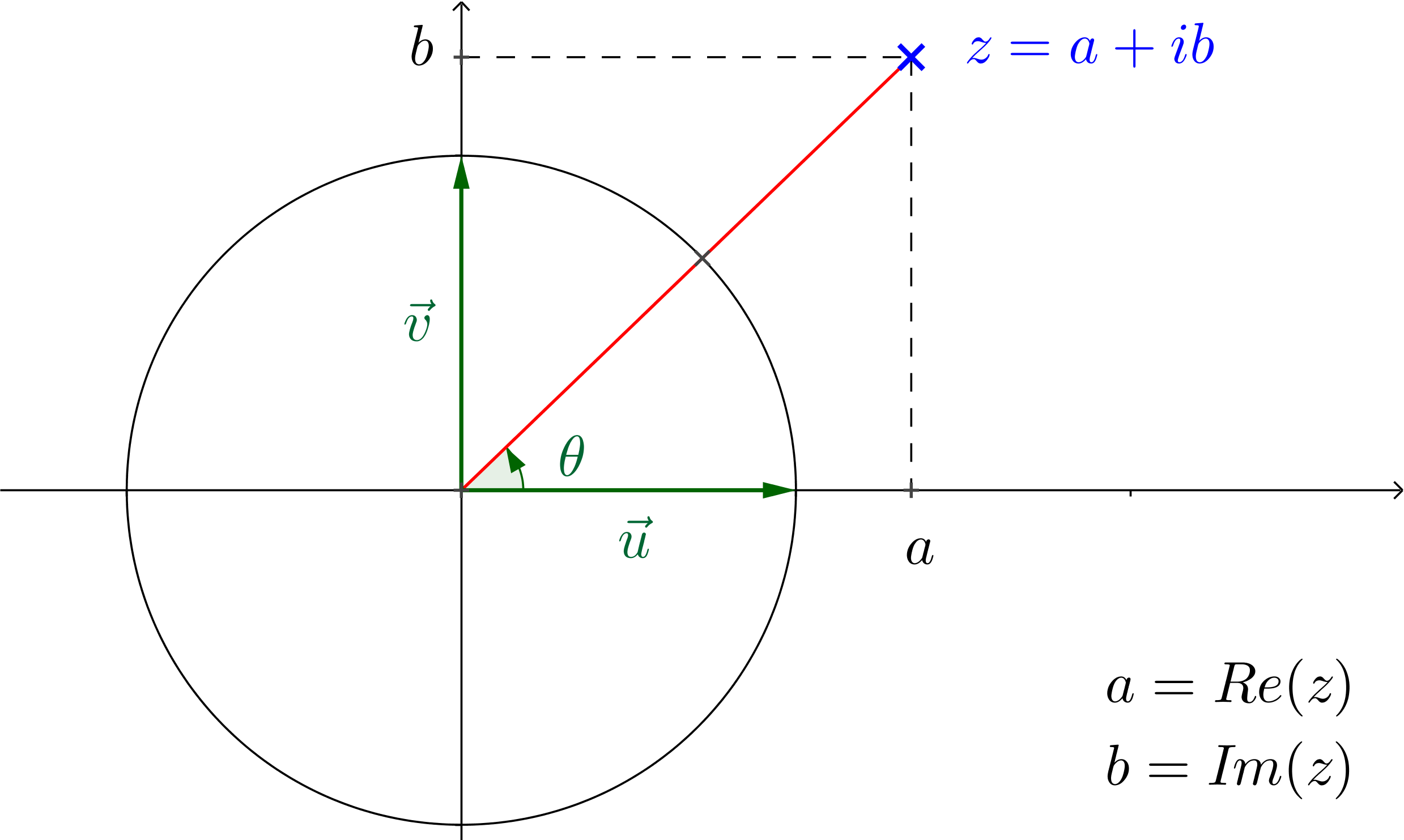 
On note :
- \( heta\) l'angle orienté \((\vec{u};\vec{OM})\).
- \(r\) la distance \(OM\)
- Si \(OM = 1\), c'est à dire, si \(M\) est sur le cercle trigonométrique, on sait que \(M\) à pour coordonnées \((cos (\theta); sin (\theta))\), et donc : $$ z=cos (\theta) + i sin (\theta) $$
- et en général, \(z=r (cos (\theta) + i sin (\theta))\)
2Définitions et propriétés
En reprenant les notations précédentes, on appelle :
- L'argument de \(z\), noté \(arg (z)\), l'angle \(\theta = (\vec{u};\vec{OM})\in[0;2\pi[\) en radian.
- Le module de \(z\), noté \(|z|\), la longueur \(OM = \sqrt{a^2+b^2}\)
Soit \(z\in\mathbb{C}\), alors \(|z|^2 = z\bar{z}\)
Soit \(z\in\mathbb{C}\), alors :
- \(arg (\bar{z}) = arg (z)\)
- \(arg (-z) = arg (z) + \pi\)
- \(|-z| = |z|\)
- \(|\bar{z}| = |z|\)
Soit \(z\in\mathbb{C}\), alors :
- Si \(z \in \mathbb{R}^+\), \(arg (z) = 0\)
- Si \(z \in \mathbb{R}^-\), \(arg (z) = \pi\)
- Si \(z \in i \mathbb{R}^+\), \(arg (z) = \frac{\pi}{2}\)
- Si \(z \in i \mathbb{R}^-\), \(arg (z) = \frac{3 \pi}{2}\)
La forme trigonométrique d'un nombre complexe non nul est : $$ z=r (cos (\theta) + i sin (\theta)) $$ où \(\theta = arg (z)\) et \(r = |z|\)
Pour passer de la forme algébrique \(z=a+ib\) à la forme trigonométrique \(z=r (cos (\theta) + i sin (\theta) )\) il faut respecter les étapes :
- Calculer le module \(r = |z|\) à l'aide de la formule \(|z| = \sqrt{a+ib}\)
- Factoriser \(z\) par \(r\) : \(z = r (\frac{a}{r} + i \frac{b}{r})\)
- Reconnaître l'angle dont le cosinus est \(\frac{a}{r}\) et le sinus est \(\frac{b}{r}\)
Exercice Résolu
On pose \(z = \sqrt{3} + i\) (forme algébrique). Mettre \(z\) sous forme trigonométrique.
Calcul du module
$$ \begin{align} r & = & \sqrt{\sqrt{3}^2 + 1^2} \\ & = & \sqrt{3 + 1} \\ & = & \sqrt{4} \\ r & = & 2 \\ \end{align} $$Factorisation par le module
On a donc \(z = 2 (\frac{\sqrt{3}}{2} + i \frac{1}{2})\)Reconnaître l'angle (chapitre trigo)
On sait que \(cos (\frac{\pi}{6}) = \frac{\sqrt{3}}{2}\) et \(sin (\frac{\pi}{6}) = \frac{1}{2}\), donc \(arg (z) = \frac{\pi}{6}\), et donc : $$ z = 2 (cos (\frac{\pi}{6}) + i sin (\frac{\pi}{6})) $$3Interprétation géométrique
Soient \(A\) et \(B\) deux points d'affixes respectives \(z_A\) et \(z_B\). Alors la distance \(AB\) vaut : $$ AB = |z_B - z_A| $$
On se place dans le repère orthonormé \((\vec{u};\vec{v})\). Soient \(A\) et \(B\) deux points distincts d'affixes respectives \(z_A\) et \(z_B\). Alors l'angle orienté \((\vec{u};\vec{AB})\) vaut : $$ (\vec{u};\vec{AB}) = arg (z_B - z_A) $$
IIForme exponentielle
1Introduction
2Définition, propriétés