- Un extremum de $f$ est une valeur maximum ou minimum de $f$
- Le maximum global est la plus grande valeur de $f(x)$ pour tout $x$ de $I$
- Le minimum global est la plus petite valeur de $f(x)$ pour tout $x$ de $I$
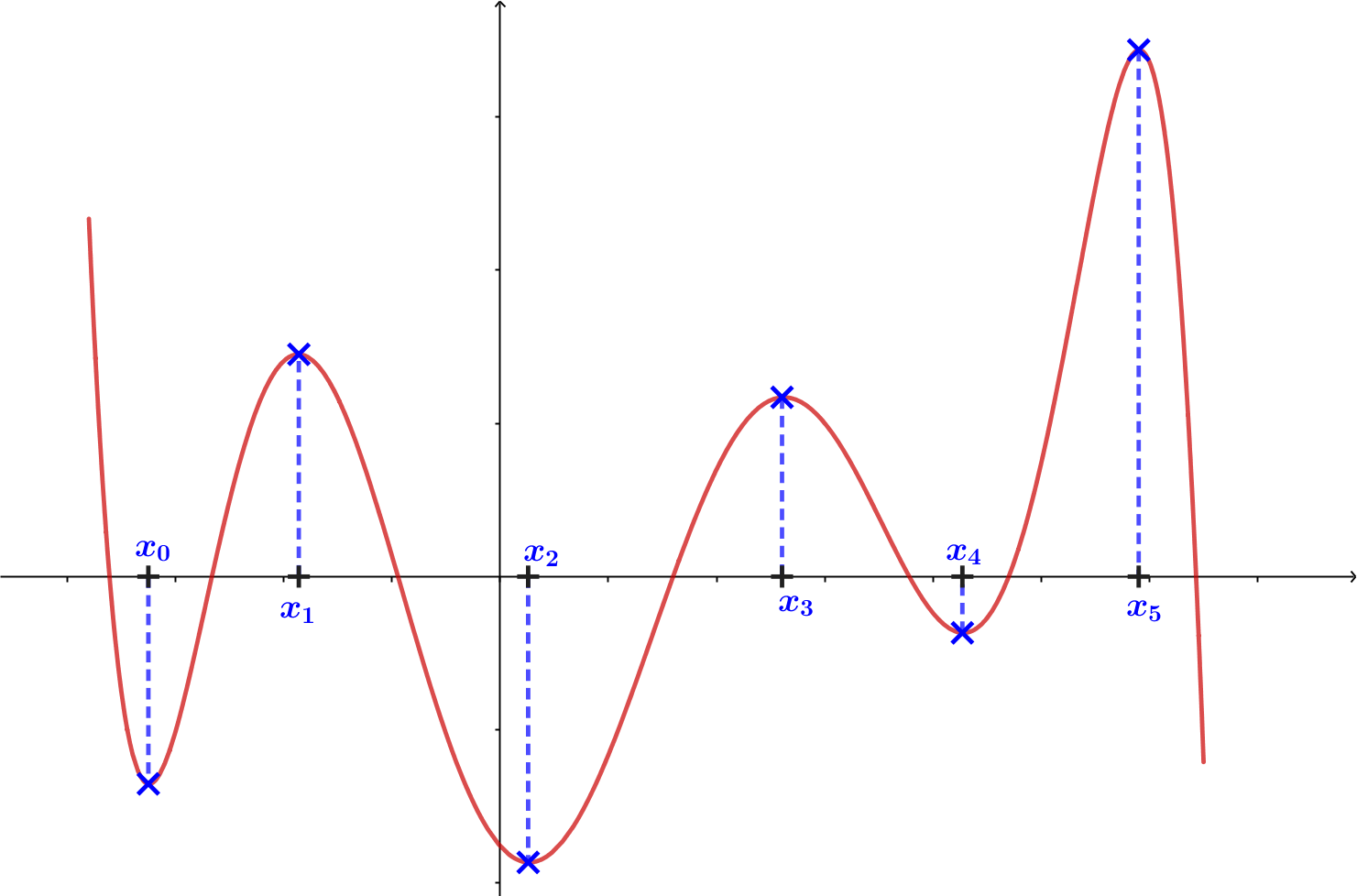
- Des maximums locaux sont atteints en $x=x_1$ et $x=x_3$
- Des minimums locaux sont atteints en $x=x_0$ et $x=x_4$
- Le maximum global est atteint en $x=x_5$
- Le minimum global est atteint en $x=x_2$
| Expression Algébrique | Cas $a\lt 0$ | Cas $a\gt 0$ |
|---|---|---|
|
|
Représentation graphique :
|
Représentation graphique :
Tableau de variation$$ \begin{array}{c|lcccr|} x &-\infty & & -b/a & & +\infty\\\\\hline f (x) & & & \nearrow\hspace{-0.4cm}0 & & \\\\ \end{array} $$ |
| Lecture graphique de l'équation | Cas $a\lt 0$ | Cas $a\gt 0$ |
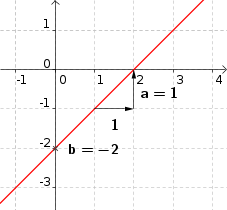
Estimation du coefficient directeur :Estimation du coefficient directeur : |
|
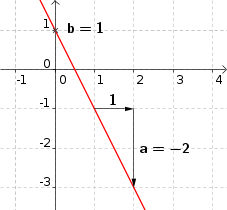
|
| Lecture graphique de l'équation | ||
|
Si la droite passe par les points $A (x_A;y_B)$ et $x_B;y_B$ : |
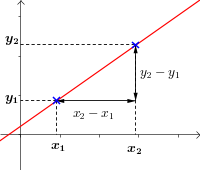
|
|
| Expression Algébrique | Représentation graphique | Tableau de variations |
|---|---|---|
|
|
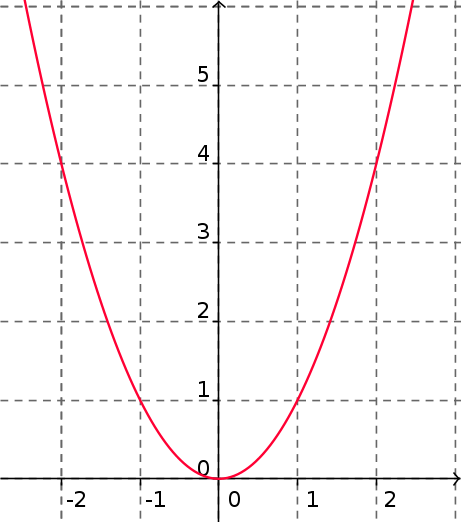
|
$$
\begin{array}{c|lcccr|}
x &-\infty & & 0 & & +\infty\\\\\hline
f (x) & & \searrow & 0 & \nearrow & \\\\
\end{array}
$$
|
Stratégie
Pour montrer qu'une fonction $f$ est croissante, il faut vérifier que si on a $a \lt b$, alors $f (a) \lt f (b)$
Départ
Soient $a$ et $b$ dans $[0;+\infty[$ tels que $a \lt b$, on essaye de montrer que $f (a) \lt f (b)$, qui revient à montrer que :
$$ f (a) - f (b) \lt 0 $$On va donc étudier le signe de $f (a) - f (b) = a^2 - b^2$
Etape astucieuse
On se souvient que $a^2 - b^2 = (a-b) (a+b)$
On édudie le signe des membres du produit :
- $a-b \lt 0$ car on a supposé au départ que $a \lt b$
- $a+b \gt 0$ car on a supposé au départ que $a$ et $b$ sont dans $[0;+\infty[$ (et donc positifs)
Conclusion
On vient de montrer que $f (a) - f (b) \lt 0$, cqfd
La fonction carré est bien croissante sur $[0;+\infty[$
| Expression Algébrique | Représentation graphique | Tableau de variations |
|---|---|---|
|
|
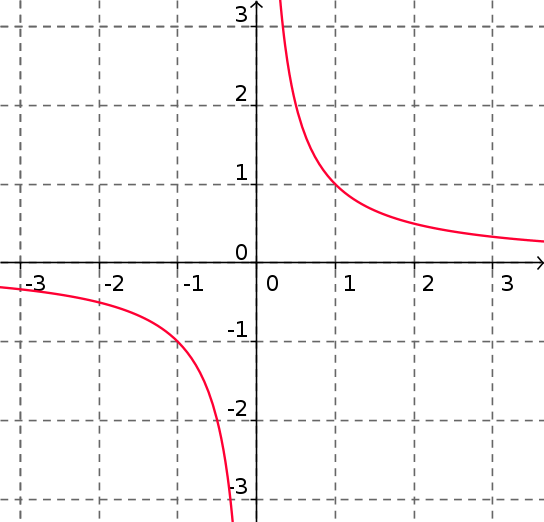
|
$$
\begin{array}{c|lcccr|}
x &-\infty & & 0 & & +\infty\\\\\hline
f (x) & & \searrow & \Vert & \searrow & \\\\
\end{array}
$$
|
| Expression Algébrique | Représentation graphique | Tableau de variations |
|---|---|---|
|
|
Représentation graphique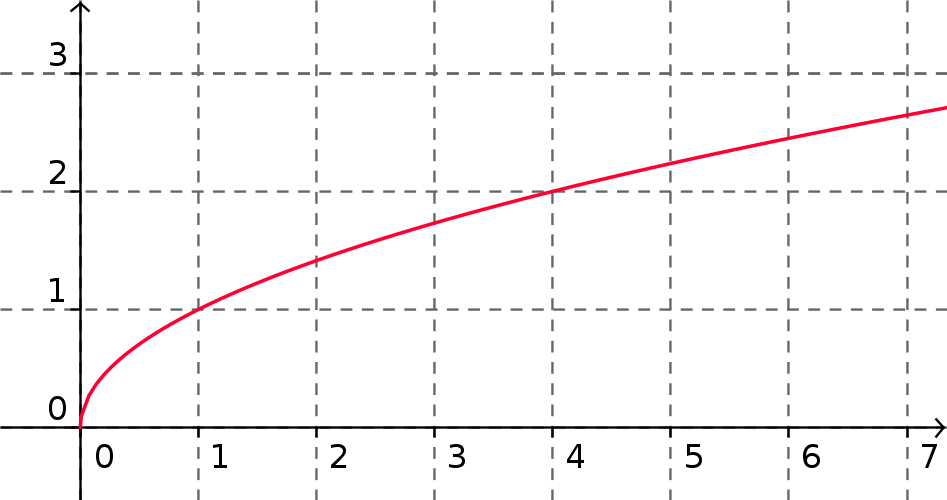
|
$$
\begin{array}{c|lcr|}
x & 0 & & +\infty\\\\\hline
f (x) & 0 & \nearrow & \\\\
\end{array}
$$
|
Stratégie
Pour montrer qu'une fonction $f$ est croissante, il faut vérifier que si on a $a \lt b$, alors $f (a) \lt f (b)$
Départ
Soient $a$ et $b$ dans $[0;+\infty[$ tels que $a \lt b$, on essaye de montrer que $f (a) \lt f (b)$, qui revient à montrer que :
$$ f (a) - f (b) \lt 0 $$On va donc étudier le signe de $f (a) - f (b) = \sqrt{a} - \sqrt{b}$
Etape astucieuse
On remarque que : $$ \begin{align} \sqrt{a} - \sqrt{b} & = & \frac{(\sqrt{a} - \sqrt{b})(\sqrt{a} + \sqrt{b})}{\sqrt{a} + \sqrt{b}} \\ & = & \frac{\sqrt{a}^2 - \sqrt{b}^2}{\sqrt{a} + \sqrt{b}} \\ & = & \frac{a - b}{\sqrt{a} + \sqrt{b}} \end{align} $$
On édudie le signe du numérateur et du dénominateur :
- $a-b \lt 0$ car on a supposé au départ que $a \lt b$
- $\sqrt{a}+\sqrt{b} > 0$ car $\sqrt{a}\gt 0$ et $\sqrt{b}\gt 0$
Conclusion
On vient de montrer que $f (a) - f (b) \lt 0$, cqfd
La fonction racine carré est bien croissante sur $[0;+\infty[$
Fonction valeur absolue $x \mapsto |x|$
| Expression Algébrique | Représentation graphique | Tableau de variations |
|---|---|---|
|
|
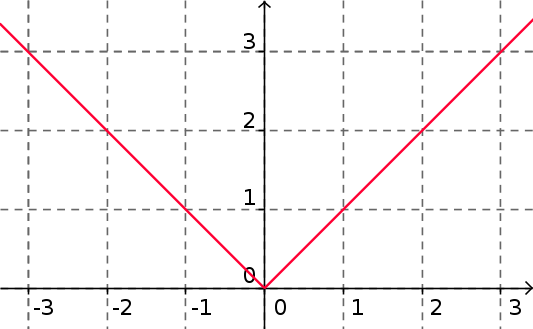
|
$$
\begin{array}{c|lcccr|}
x &-\infty & & 0 & & +\infty\\\\\hline
f (x) & & \searrow & 0 & \nearrow & \\\\
\end{array}
$$
|
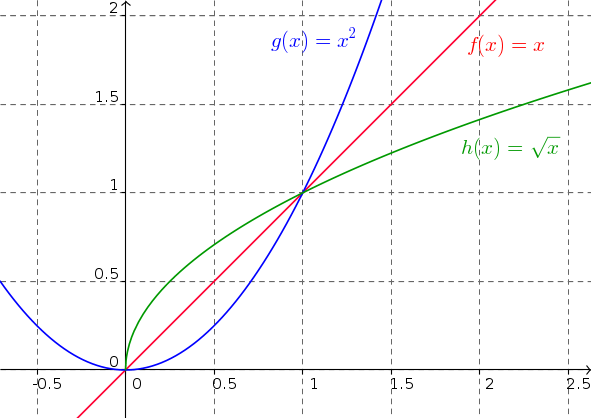
- $f (1) = 1$, $g (1) = 1^2 = 1$ et $h (1) = \sqrt{1} = 1$
- $f (0) = 0$, $g (0) = 0^2 = 0$ et $h (0) = \sqrt{0} = 0$
- Sur $]-\infty;0[$, la droite $C_f$ est en dessous de $C_g$
- Sur $]0;1[$, la droite $C_f$ est au dessus de $C_g$
- Sur $]0;+\infty[$, la droite $C_f$ est en dessous de $C_g$
Stratégie
On cherche à connaître les valeurs $x$ pour lesquelles la droite $C_g$ est au dessus de la courbe $C_f$, c'est à dire les $x$ vérifiant $g (x) \gt f (x)$.Mise en forme
On résoud l'inéquation $g (x) \gt f (x)$ : $$ \begin{array}{cl} & g (x) \gt f (x) \\\\ \Leftrightarrow & x^2 \lt x \\\\ \Leftrightarrow & x^2 - x \lt 0 \\\\ \Leftrightarrow & x (x - 1) \lt 0 \end{array} $$
Résolution
On étudie le signe du produit : $$ \begin{array}{c|lcccccr|} x &-\infty & & 0 & & 1 & & +\infty\\\\\hline x & & - & |\hspace{-0.15cm}0 & + & & + & \\\\ \hline x -1 & & - & & - & |\hspace{-0.15cm}0 & + & \\\\ \hline x (x -1) & & + & |\hspace{-0.15cm}0 & - & |\hspace{-0.15cm}0 & + & \\\\ \hline \end{array} $$Conclusion
- $g (x) \gt f (x)$ sur $ ]-\infty;0[\cup]1;+\infty[$ (courbe $C_g$ au dessus de la droite $C_d$).
- $g (x) \lt f (x)$ sur $ ]0;1[$ (courbe $C_g$ sous la droite $C_f$).
- Sur $]0;1[$, la droite $C_f$ est en dessous de $C_h$
- Sur $]0;+\infty[$, la droite $C_f$ est au dessus de $C_h$
Stratégie
On cherche à connaître les valeurs $x$ pour lesquelles la droite $C_f$ est en dessous de la courbe $C_h$, c'est à dire les $x$ vérifiant $f (x) \lt h (x)$.Mise en forme
On résoud l'inéquation $f (x) \lt h (x)$ : $$ \begin{array}{cl} & f (x) \lt g (x) \\\\ \Leftrightarrow & x \lt \sqrt{x} \\\\ \Leftrightarrow & x - \sqrt{x} \lt 0 \\\\ \Leftrightarrow & \frac{(x - \sqrt{x})(x + \sqrt{x})}{x + \sqrt{x}} \lt 0 \\\\ \Leftrightarrow & \frac{x^2 - x}{x + \sqrt{x}} \lt 0 \\\\ \end{array} $$
Résolution
On étudie le signe du quotient :- Le dénominateur $x + \sqrt{x}$ est positif sur $[0;+\infty$
- Le signe du numérateur $x^2 - x$a déjà été étudié dans la démonstration précédente.
Conclusion
- $f (x) \lt h (x)$ sur $ ]0;1[$ (droite $C_f$ sous la courbe $C_g$).
- $f (x) \gt h (x)$ sur $ ]1;+\infty[$ (droite $C_f$ au dessus de la courbe $C_g$).
- Sur $]0;1[$, la courbe $C_g$ est en dessous de $C_h$
- Sur $]0;+\infty[$, la courbe $C_f$ est au dessus de $C_h$
- Sur $]0;1[$, on sait que $g (x) \lt f (x)$ et que $f (x) \lt h (x)$, donc $g (x) \lt h (x)$
- Sur $]0;+\infty[$, on sait que $h (x) \lt f (x)$ et que $f (x) \lt g (x)$, donc $h (x) \lt g (x)$