|
|

|
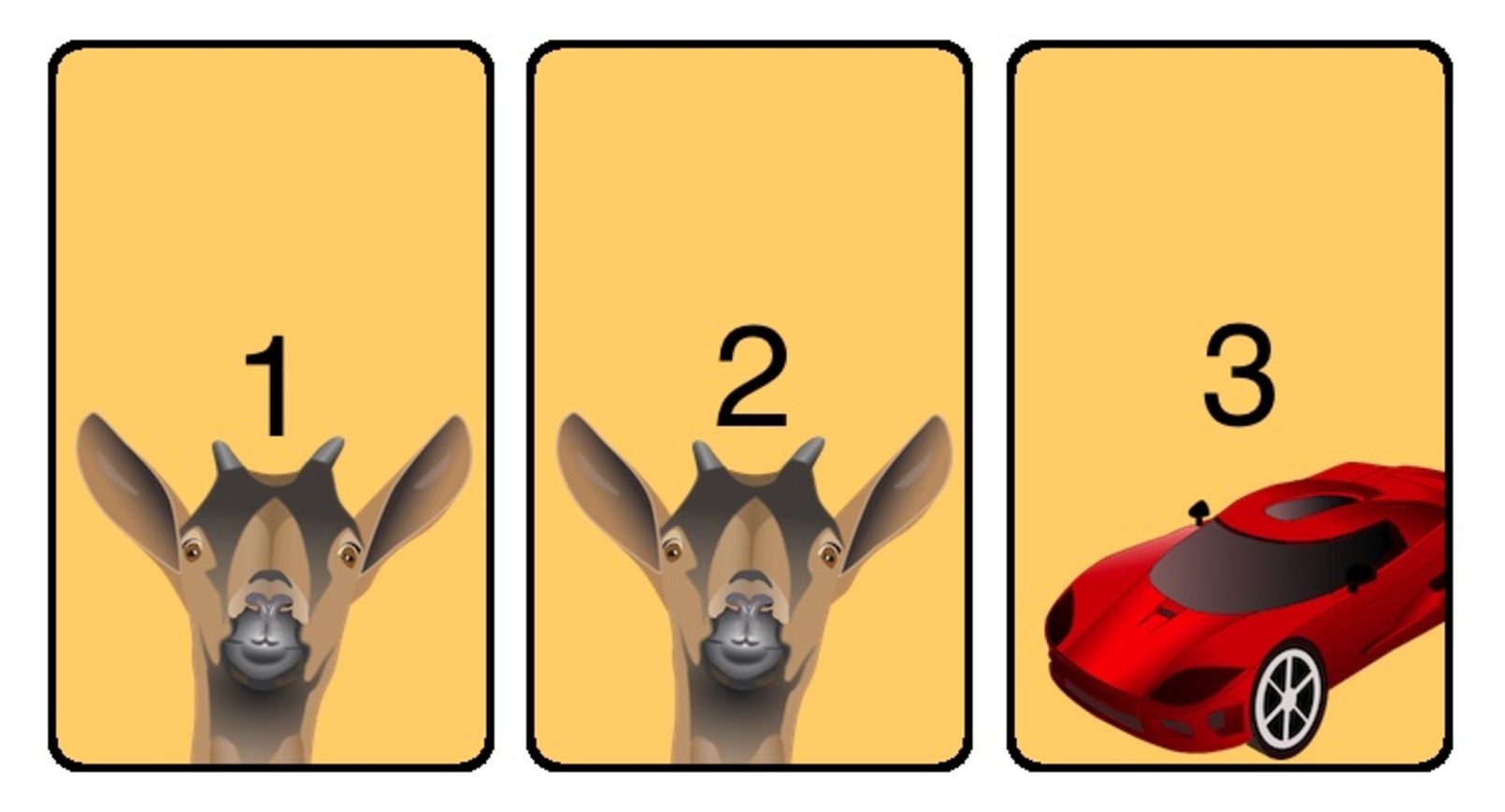
Le choix se déroule en deux temps :
|



- $V$ : « le joueur choisit la porte de la voiture »
- $A_1$ : « le joueur choisit la porte de la première chèvre »
- $A_2$ : « le joueur choisit la porte de la deuxième chèvre »
- $B_1$ : « Monty Hall retire la première chèvre »
- $B_2$ : « Monty Hall retire la deuxième chèvre »
Le problème de Monthy Hall fait partie de ces jeux changés ou abandonnés après que des mathématiciens l'ont étudié.
Un autre exemple connu est celui du "black jack" (jeu de carte) pour lequel quelques étudiants du MITUn film, plus ou moins fidèle, Las Vegas 21 y est consacré :
Si ici les probabilités ont mis en évidence un déséquilibre innocent dans les règles d'un jeu télévisé, elles peuvent aussi être utilisées pour dévoiler des arnaques ou des abus de "faux-magiciens". Cette démarche s'appelle la zététique et encourage la pensée critique :