 Vous souvenez vous qu'un vecteur peut représenter un déplacement ? Qu'il a une norme ou longueur, une direction, et un sens ? Qu'il est aussi possible d'additionner des vecteurs ou de les multiplier par un nombre réel ?
Vous souvenez vous qu'un vecteur peut représenter un déplacement ? Qu'il a une norme ou longueur, une direction, et un sens ? Qu'il est aussi possible d'additionner des vecteurs ou de les multiplier par un nombre réel ?
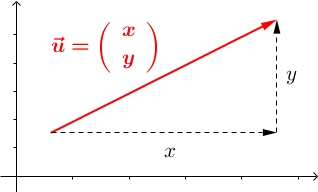 Coordonnées $\vec{u} = \left(\begin{array}{c} x \\ y \end{array}\right)$
Coordonnées $\vec{u} = \left(\begin{array}{c} x \\ y \end{array}\right)$
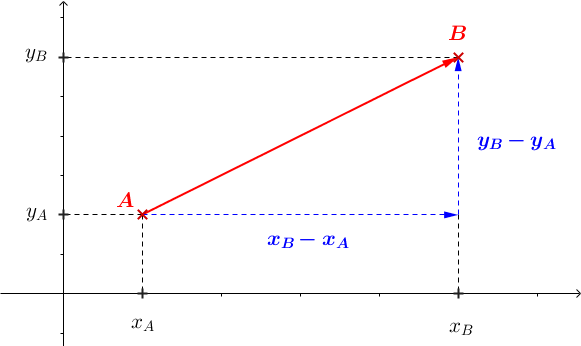 $\vec{AB} = \left ( \begin{array}{c} x_B - x_A \\ y_B - y_A \end{array} \right)$
$\vec{AB} = \left ( \begin{array}{c} x_B - x_A \\ y_B - y_A \end{array} \right)$
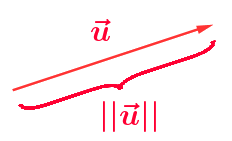 Norme $||\vec{u}|| = \sqrt{x^2+y^2}$
Norme $||\vec{u}|| = \sqrt{x^2+y^2}$
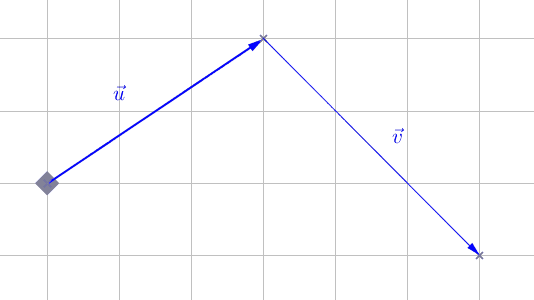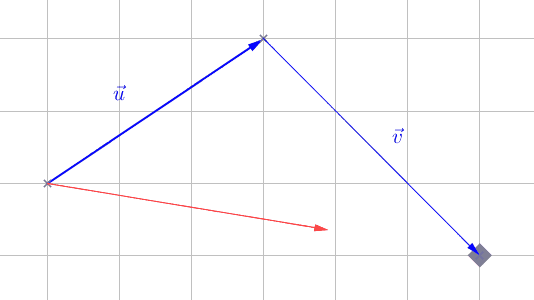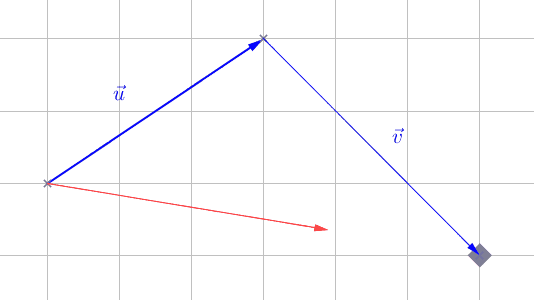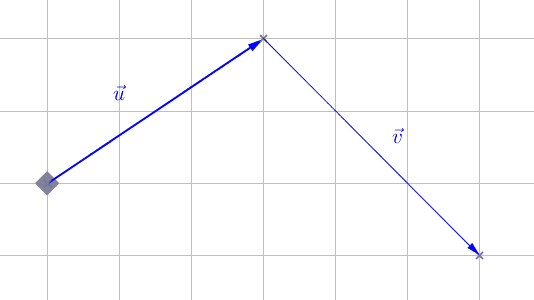 Vecteur somme $\vec{u}+\vec{v} = \left(\begin{array}{c} x+x' \\ y+y' \end{array}\right)$
Vecteur somme $\vec{u}+\vec{v} = \left(\begin{array}{c} x+x' \\ y+y' \end{array}\right)$
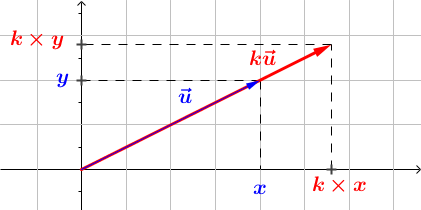 Produit par un réel $k \vec{u} = \left(\begin{array}{c} k x \\ k y \end{array}\right)$
Produit par un réel $k \vec{u} = \left(\begin{array}{c} k x \\ k y \end{array}\right)$

Cours de seconde sur les vecteurs. Coordonnées, égalité, opposé, somme (ancien site, ça pique un peu...)

Cours de seconde sur la colinéarité des vecteurs. Multiplication par un réel (ancien site aussi)
Entrons maintenant dans le vid du sujet ; le produit scalaire de $\color{blue}{\vec{u}}$ par $\color{red}{\vec{v}}$, que l'on note $\color{blue}{\vec{u}}.\color{red}{\vec{v}}$ (avec un point). Son résultat est un nombre (et pas un vecteur) qui, intuitivement, peut être compris comme ceci :
$$ \begin{array}{ccl} \color{red}{\vec{u}} . \color{blue}{\vec{v}} &=& \begin{array}{cc}\text{"A quel point les vecteurs $\color{blue}{\vec{u}}$ et } \color{red}{\vec{v}} \\ \text{ travaillent t'ils ensemble ?" } \end{array} \end{array} $$
 Certes cette définition n'est pas très précise, mais prenons notre temps. Dans l'exemple ci-dessous,
Certes cette définition n'est pas très précise, mais prenons notre temps. Dans l'exemple ci-dessous,  se déplace horizontalement suivant $\color{red}{\vec{v}}$ (de $A$ jusqu'à $B$) et se fait tracter par
se déplace horizontalement suivant $\color{red}{\vec{v}}$ (de $A$ jusqu'à $B$) et se fait tracter par  avec une force $\color{blue}{\vec{u}}$. Essayez de faire varier les vecteurs $\color{blue}{\vec{u}}$ et $\color{red}{\vec{v}}$ pour observer les conséquences sur la course de
avec une force $\color{blue}{\vec{u}}$. Essayez de faire varier les vecteurs $\color{blue}{\vec{u}}$ et $\color{red}{\vec{v}}$ pour observer les conséquences sur la course de  :
:
la course de
 est rapide
est rapide
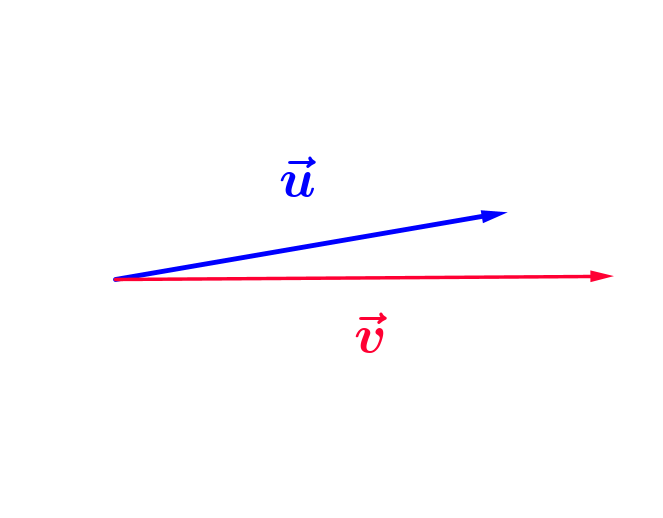 Dans ce cas, la valeur de $\vec{u}.\vec{v}$ doit être élevée.
Dans ce cas, la valeur de $\vec{u}.\vec{v}$ doit être élevée.
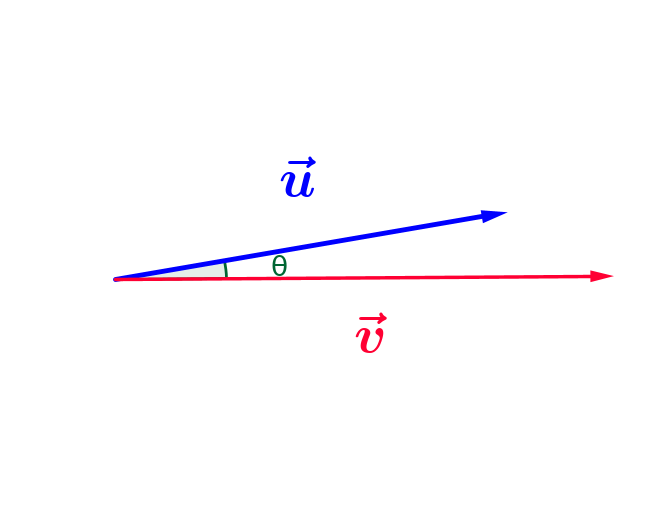
 est maximale
est maximale quand les vecteurs ont la même direction (colinéaires)
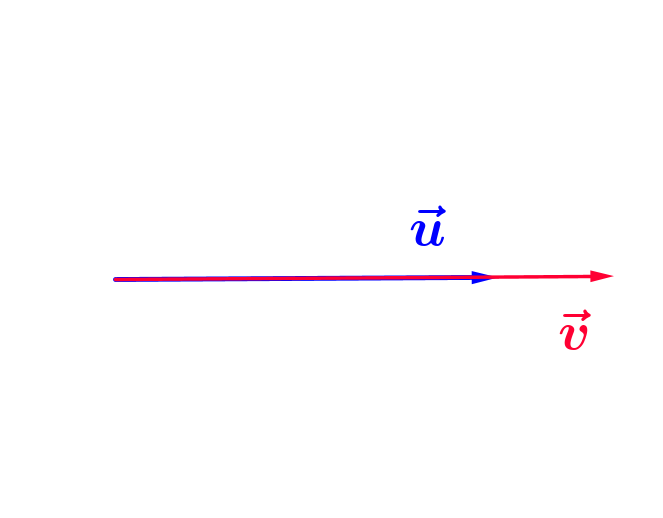 La valeur du produit scalaire doit être encore plus grande
La valeur du produit scalaire doit être encore plus grande
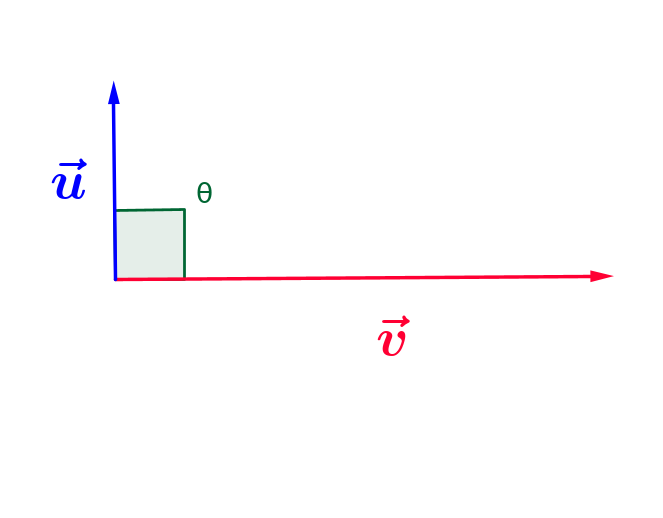 Dans ce cas, $\color{blue}{\vec{u}}.\color{red}{\vec{v}}=0$
Dans ce cas, $\color{blue}{\vec{u}}.\color{red}{\vec{v}}=0$
la direction de $\color{red}{v}$, et un autre $\color{blue}{\vec{u_y}}$ orthogonal :
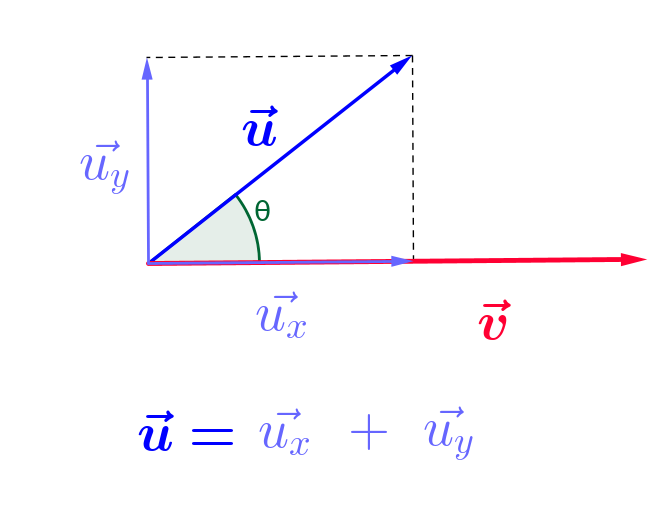 De cette manière, on comprend que c'est la composante $\color{blue}{\vec{u_x}}$
De cette manière, on comprend que c'est la composante $\color{blue}{\vec{u_x}}$ qui travaille avec $\color{red}{\vec{v}}$, alors que $\color{blue}{\vec{u_y}}$ n'a aucun effet.
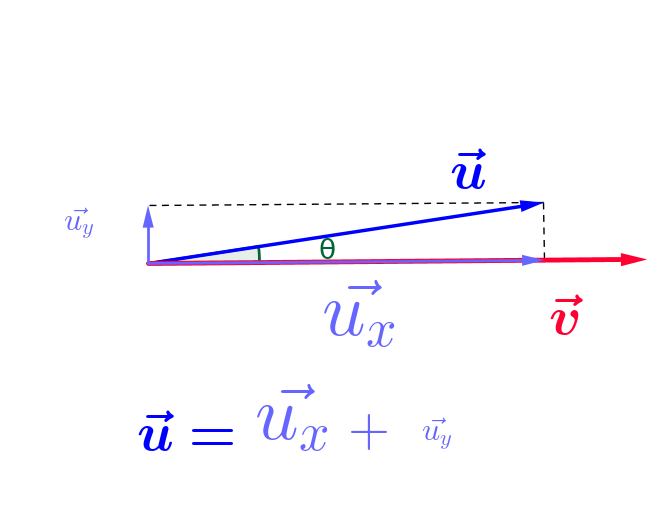 Ce qui explique la plus grande vitesse de
Ce qui explique la plus grande vitesse de 
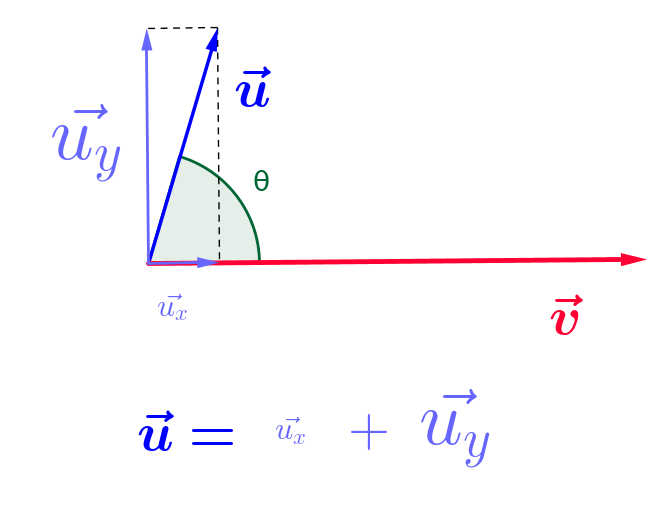 ...et
...et  ralentit !
ralentit !
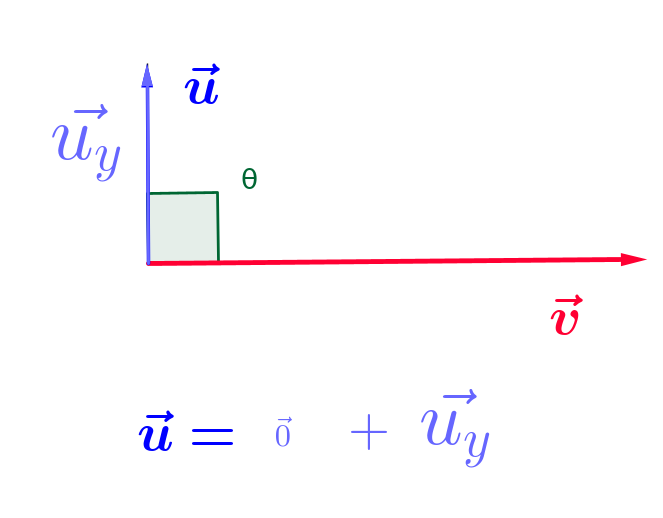 ...et donc
...et donc  fait du sur-place.
fait du sur-place.
avec celle du trajet $\color{red}{\vec{v}}$.
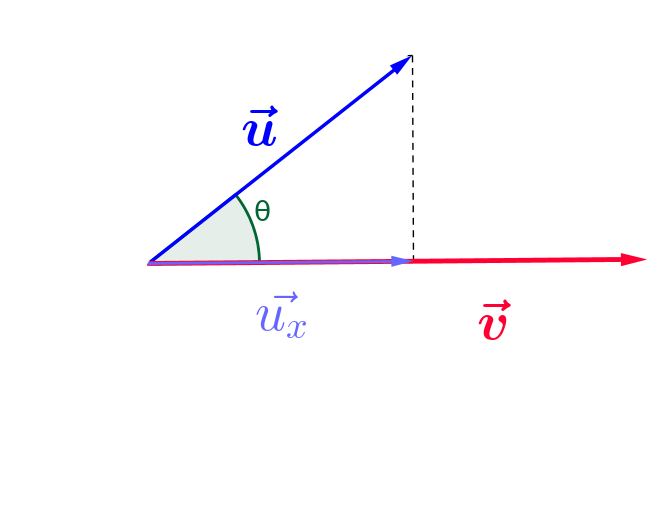 Il est donc à la fois proportionnel à $\color{blue}{||\vec{u_x}||}$ et $\color{red}{||\vec{v}||}$
Il est donc à la fois proportionnel à $\color{blue}{||\vec{u_x}||}$ et $\color{red}{||\vec{v}||}$
estime le "travail commun" de $\color{blue}{\vec{u}}$ et $\color{red}{\vec{v}}$ est par la formule ci-dessous :
 $\color{blue}{\vec{u}}.\color{blue}{\vec{v}} = ||\color{blue}{\vec{u_x}}|| \times ||\color{red}{\vec{v}}||$
$\color{blue}{\vec{u}}.\color{blue}{\vec{v}} = ||\color{blue}{\vec{u_x}}|| \times ||\color{red}{\vec{v}}||$
ci-dessous d'hypothénuse $||\color{blue}{\vec{u}}||$, de côté adjacent $||\color{blue}{\vec{u_x}}||$ et d'angle $\color{green}{\theta}$ :
 $\color{green}{cos(\theta)} = \frac{ ||\color{blue}{\vec{u_x}}||}{ ||\color{blue}{\vec{u}}||}$, donc $||\color{blue}{\vec{u_x}}|| = ||\color{blue}{\vec{u}}|| \times \color{green}{cos(\theta)}$
$\color{green}{cos(\theta)} = \frac{ ||\color{blue}{\vec{u_x}}||}{ ||\color{blue}{\vec{u}}||}$, donc $||\color{blue}{\vec{u_x}}|| = ||\color{blue}{\vec{u}}|| \times \color{green}{cos(\theta)}$
et donc $\color{blue}{\vec{u}}.\color{blue}{\vec{v}} = ||\color{blue}{\vec{u}}|| ||\color{red}{\vec{v}}|| \color{green}{cos(\theta)}$
 L'angle $\color{green}{\theta} = 0$, donc $\color{green}{cos(\theta)=1}$ et donc le produit scalaire est maximal :
L'angle $\color{green}{\theta} = 0$, donc $\color{green}{cos(\theta)=1}$ et donc le produit scalaire est maximal : $\color{blue}{\vec{u}}.\color{blue}{\vec{v}} = ||\color{blue}{\vec{u}}|| ||\color{red}{\vec{v}}||\times 1 = ||\color{blue}{\vec{u}}|| ||\color{red}{\vec{v}}||$
 L'angle $\color{green}{\theta} = \frac{\pi}{2}$, donc $\color{green}{cos(\theta)=0}$ et donc le produit scalaire est nul :
L'angle $\color{green}{\theta} = \frac{\pi}{2}$, donc $\color{green}{cos(\theta)=0}$ et donc le produit scalaire est nul : $\color{blue}{\vec{u}}.\color{blue}{\vec{v}} = ||\color{blue}{\vec{u}}|| ||\color{red}{\vec{v}}||\times 0 = 0 $
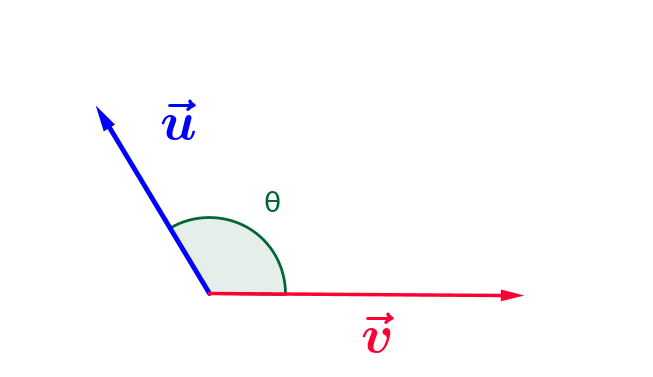
 et donc $\color{blue}{\vec{u}}.\color{blue}{\vec{v}} = ||\color{blue}{\vec{u}}|| ||\color{red}{\vec{v}}|| \color{green}{cos(\theta}) \lt 0$
et donc $\color{blue}{\vec{u}}.\color{blue}{\vec{v}} = ||\color{blue}{\vec{u}}|| ||\color{red}{\vec{v}}|| \color{green}{cos(\theta}) \lt 0$ et
 part dans l'autre sens :)
part dans l'autre sens :)
d'où sort la formule du produit scalaire et d'en avoir une petite intuition...

 a estimé pour vous leur niveau d'utilité avec une système d'étoiles
a estimé pour vous leur niveau d'utilité avec une système d'étoiles  .
.
 La première définition correspond à l' explication dans l'introduction : deux vecteurs $\vec{u}$ et $\vec{v}$ travaillent mieux ensemble quand ils sont dans la même direction. Et c'est donc le projeté orthogonal $\vec{u_x}$ qui travaille effectivement avec $\vec{v}$ :
La première définition correspond à l' explication dans l'introduction : deux vecteurs $\vec{u}$ et $\vec{v}$ travaillent mieux ensemble quand ils sont dans la même direction. Et c'est donc le projeté orthogonal $\vec{u_x}$ qui travaille effectivement avec $\vec{v}$ :
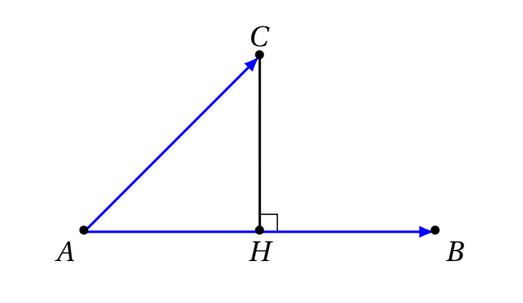
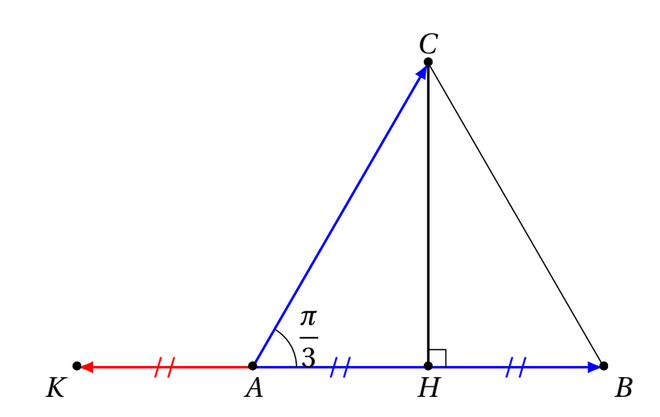
 Soit $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs non-nuls, et trois points $A,B$ et $C$ tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$. Le produit scalaire de $\overrightarrow{u}$ et $\overrightarrow{v}$, noté $\overrightarrow{u}.\overrightarrow{v}$ est définir comme suit:
$$\overrightarrow{u}.\overrightarrow{v}=\left\{\begin{array}{lr}
AB\times AH & \text{si}\quad (\overrightarrow{AH},\overrightarrow{AB})=0 \\
-AB\times AH & \text{si}\quad (\overrightarrow{AH},\overrightarrow{AB})=\pi
\end{array} \right.$$
Où $H$ est le projeté orthogonal du points $C$ sur la droite $(AB)$
Soit $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs non-nuls, et trois points $A,B$ et $C$ tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$. Le produit scalaire de $\overrightarrow{u}$ et $\overrightarrow{v}$, noté $\overrightarrow{u}.\overrightarrow{v}$ est définir comme suit:
$$\overrightarrow{u}.\overrightarrow{v}=\left\{\begin{array}{lr}
AB\times AH & \text{si}\quad (\overrightarrow{AH},\overrightarrow{AB})=0 \\
-AB\times AH & \text{si}\quad (\overrightarrow{AH},\overrightarrow{AB})=\pi
\end{array} \right.$$
Où $H$ est le projeté orthogonal du points $C$ sur la droite $(AB)$
 Si $\overrightarrow{u}$ ou $\overrightarrow{v}$ est nul, alors $\overrightarrow{u}.\overrightarrow{v}=0$
Si $\overrightarrow{u}$ ou $\overrightarrow{v}$ est nul, alors $\overrightarrow{u}.\overrightarrow{v}=0$
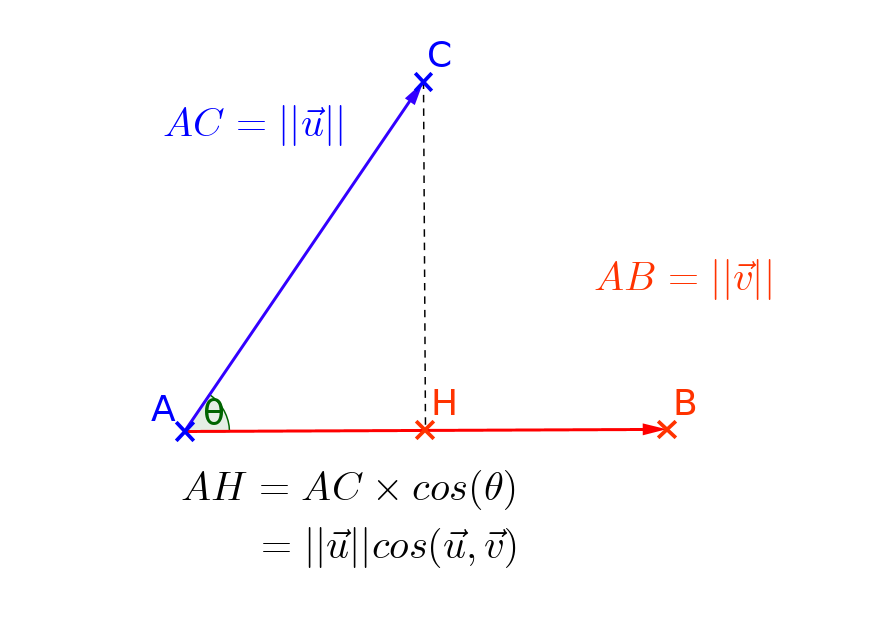
 Soit $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs non nuls, le produit scalaire de $\overrightarrow{u}$ et $\overrightarrow{v}$ peut se calculer comme suit:
\[ \overrightarrow{u}.\overrightarrow{v}=||\overrightarrow{u}||\times||\overrightarrow{v}||\times \cos\left(\overrightarrow{u},\overrightarrow{v}\right) \]
Soit $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs non nuls, le produit scalaire de $\overrightarrow{u}$ et $\overrightarrow{v}$ peut se calculer comme suit:
\[ \overrightarrow{u}.\overrightarrow{v}=||\overrightarrow{u}||\times||\overrightarrow{v}||\times \cos\left(\overrightarrow{u},\overrightarrow{v}\right) \]
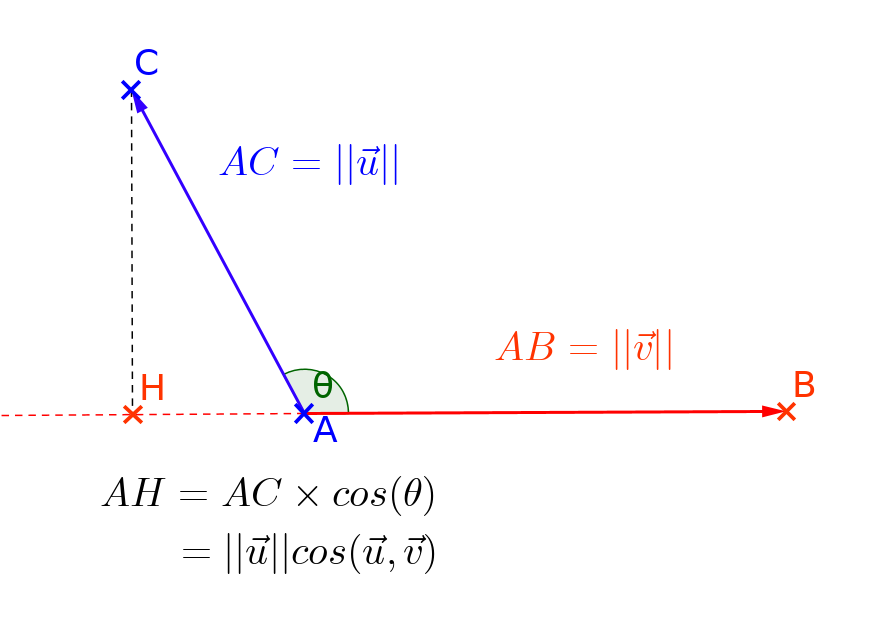
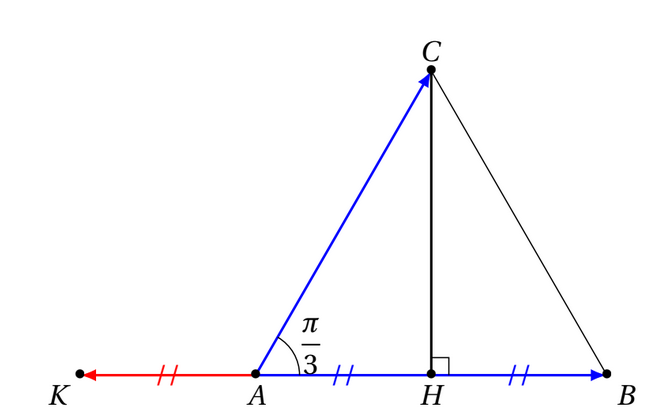
 ) s'utilisera le plus souvent à l'envers. C'est à dire pour retrouver l'angle quand on connaît déjà le produit scalaire (grâce à la boss des formules, la numéro 4).
) s'utilisera le plus souvent à l'envers. C'est à dire pour retrouver l'angle quand on connaît déjà le produit scalaire (grâce à la boss des formules, la numéro 4).
 Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$,
$$
\begin{array}{lll}
\left(\overrightarrow{u}.\overrightarrow{v}\right)&=&\dfrac{1}{2}\left[ ||\overrightarrow{u}+\overrightarrow{v}||^2-||\overrightarrow{u}||^2-||\overrightarrow{v}||^2 \right]\\
&=&\dfrac{1}{2}\left[ ||\overrightarrow{u}||^2+||\overrightarrow{v}||^2-||\overrightarrow{u}-\overrightarrow{v}||^2 \right]
\end{array}
$$
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$,
$$
\begin{array}{lll}
\left(\overrightarrow{u}.\overrightarrow{v}\right)&=&\dfrac{1}{2}\left[ ||\overrightarrow{u}+\overrightarrow{v}||^2-||\overrightarrow{u}||^2-||\overrightarrow{v}||^2 \right]\\
&=&\dfrac{1}{2}\left[ ||\overrightarrow{u}||^2+||\overrightarrow{v}||^2-||\overrightarrow{u}-\overrightarrow{v}||^2 \right]
\end{array}
$$
1er cas : $\vec{u} = \vec{0}$
$\overrightarrow{u}=\overrightarrow{0}$. Les trois expressions sont alors nulles, l'égalité est donc vérifiée.2ème cas : $\vec{u} \neq \vec{0}$
Nous allons commencer par construire un repère adapté au problème:
Fixons un point $A$ quelconque comme origine du repère.
Soit $I$ tel que $\overrightarrow{AI}=\dfrac{1}{||\overrightarrow{u}||}\overrightarrow{u}$ et $J$ tel que $(A,I,J)$ soit un repère orthonormé.
Dans ce repère $\overrightarrow{u}\left(\begin{array}{l}||\overrightarrow{u}||\\0\end{array}\right)$ et $\overrightarrow{v}\left(\begin{array}{ll}||\overrightarrow{v}||\cos\left(\overrightarrow{u},\overrightarrow{v}\right) ||\overrightarrow{v}||\sin\left(\overrightarrow{u},\overrightarrow{v}\right)\end{array}\right)$
DoncLa deuxième égalité se démontre en appliquant la formule aux vecteurs $\overrightarrow{u}$ et $-\overrightarrow{v}$
 Cette formule simple permettra de calculer le produit scalaire à partir des coordonnées des vecteurs ou des points d'un problème...
Cette formule simple permettra de calculer le produit scalaire à partir des coordonnées des vecteurs ou des points d'un problème...
 Le plan est munit d'un repère orthonormé. Soit $\overrightarrow{u}\left(\begin{array}{l}x\\y
\end{array}\right)$ et $\overrightarrow{v}\left(\begin{array}{l}x'\\y'
\end{array}\right)$, on a alors:
\[ \overrightarrow{u}.\overrightarrow{v}=xx'+yy'\]
Le plan est munit d'un repère orthonormé. Soit $\overrightarrow{u}\left(\begin{array}{l}x\\y
\end{array}\right)$ et $\overrightarrow{v}\left(\begin{array}{l}x'\\y'
\end{array}\right)$, on a alors:
\[ \overrightarrow{u}.\overrightarrow{v}=xx'+yy'\]
Soit $(O,I,J)$ un repère orthonormé et $\overrightarrow{u}\left(\begin{array}{c}4\\-5 \end{array}\right)$ et $\overrightarrow{v}\left(\begin{array}{l}0\\1 \end{array}\right)$.
Calculez le produit scalaire $\overrightarrow{u}.\overrightarrow{v}$
- Symétrie : $\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u}$
- Linéarité: $\overrightarrow{u}.\left(\overrightarrow{v}+\overrightarrow{w}\right)=\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{u}.\overrightarrow{w}$
-
Identités remarquables :
- $\left(\overrightarrow{u}+\overrightarrow{v}\right)^2=\overrightarrow{u}^2+2\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{v}^2$
- $\left(\overrightarrow{u}-\overrightarrow{v}\right)^2=\overrightarrow{u}^2-2\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{v}^2$
- $\left(\overrightarrow{u}+\overrightarrow{v}\right)\left(\overrightarrow{u}-\overrightarrow{v}\right)=\overrightarrow{u}^2-\overrightarrow{v}^2$
 ... enfin, des application géométriques simples mais néanmoins fondamentales et diverses !
... enfin, des application géométriques simples mais néanmoins fondamentales et diverses !
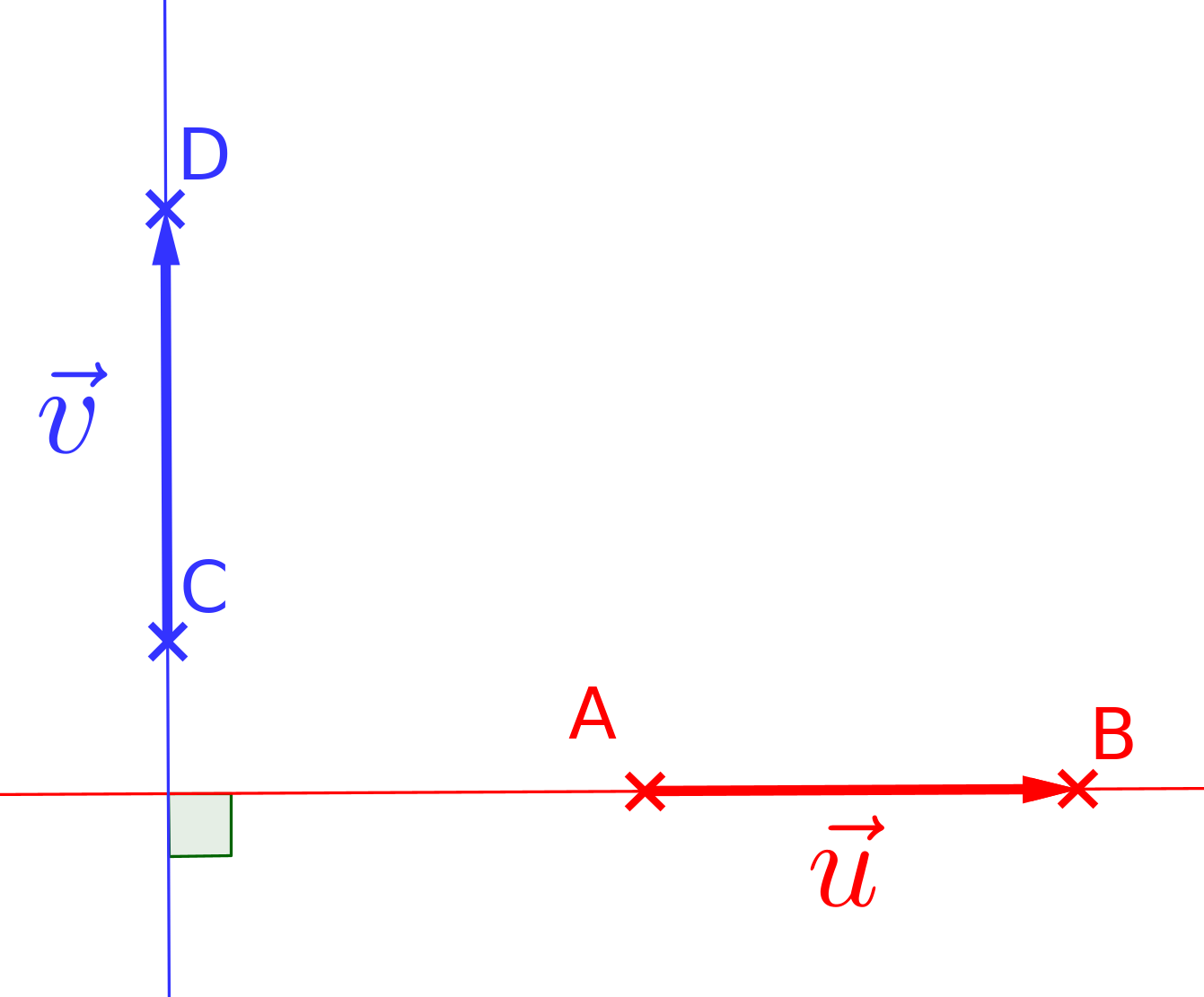 Les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont dits orthogonaux lorsque les droites $(AB)$ et $(CD)$ sont perpendiculaires.
On note souvent cela : $$ \overrightarrow{u} \perp \overrightarrow{v}$$
Les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont dits orthogonaux lorsque les droites $(AB)$ et $(CD)$ sont perpendiculaires.
On note souvent cela : $$ \overrightarrow{u} \perp \overrightarrow{v}$$
- $||\overrightarrow{u}||^2 = ||\overrightarrow{AB}||^2=AB^2$
- $||\overrightarrow{v}||^2 = ||\overrightarrow{AC}||^2=AC^2$
- $||\overrightarrow{u}-\overrightarrow{v}||^2 = ||\overrightarrow{AB}-\overrightarrow{AC}||^2 = ||\overrightarrow{CB}||^2=BC^2$
On conclut donc $\overrightarrow{u}.\overrightarrow{v}=0\Leftrightarrow \overrightarrow{u} \perp \overrightarrow{v}$
