Polynômes du second degré
Nous abordons dans ce chapitre les fameux polynômes du second degré. Un nom compliqué qui pourrait effrayer... En fait, ils sont l'étape naturelle après l'étude des fonction affines que vous connaissez déjà et qui n'étaient en fait que des polynômes du premier degré !

Pour faire simple, dans les fonctions affines (premier degré), nous avions des nombres et des x. Dans le second degré, nous y ajouterons des x². Je vous laisse imaginer ce qu'on ajoute à des polynômes de degrés supérieurs...

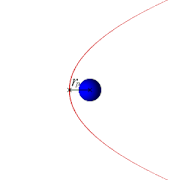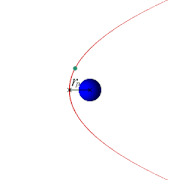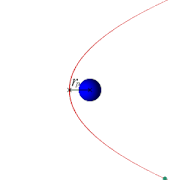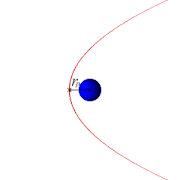
Mais c'est un autre sujet. Vous pouvez bouger les curseurs ci-dessous pour visualiser des courbes de polynômes du second degré (ou de fonctions affines quand a vaut 0 !) :

Les courbes ci-dessus s'appellent des paraboles. La forme de ces courbes permet par exemple aux antennes paraboliques une bonne réception des ondes car elle a la propriété géométrique de faire converger les ondes réfléchies en un point appelé le foyer. C'est également cette propriété géométrique qui permet d'allumer rapidement un feu avec un miroir parabolique ou de diriger la lumière des phares de voiture. Les paraboles sont également très importantes en mécanique classique de la gravitation. Autrement dit, pour représenter des trajectoires d'objets comme les comètes, mais aussi sur Terre, d'objets qui tombent, sautent ou sont lancés. Vous avez d'ailleurs peut-être déjà entendu parler des vols paraboliques qui permettent de simuler une micropesanteur pendant quelques secondes. Vous l'aurez compris, les fonctions polynôme du second degré ont de nombreuses applications. Le but de ce chapitre sera de mieux connaître leurs propriétés mathématiques dont les applications sont nombreuses en mécanique, optique, géométrie et même en économie !
On appelle fonction polynôme du second degré ou trinôme du second degré tout fonction définie sur $\mathbb{R}$ par : $$f (x) = a x^2 + b x + c $$ où $a, b, c $ sont trois nombres réels. La fonction carré définie par $f (x) = x^2$ est une fonction polynôme du second degré ($a=1, b=0, c=0$).
Soient, $a, x_1, x_2$ des nombres réels. La fonction $f$ définie ci-dessous est un polynôme du second degré : $$ f(x) = a (x-x_1)(x-x_2), \text{ pour tout } x \in \mathbb{R} $$ En effet, si on développe $f$, on retrouve sa forme développée : $$ \begin{array}{ccl} f (x) &=& a (x-x_1)(x-x_2) \\\\ &=& a\left(x^2 - x_2 x - x_1 x - x1 x_2\right \\\\ &=& a x^2 - a(x_2 +x_1) x - a x_1 x_2 \end{array} $$ $f$ est bien un polynôme du second degré avec $b = a (x_1 + x_2)$ et $c= ax_1 x_2$ On reprend la fonction $f$ définie dans la propriété précédente :
  • $f$ est la forme développée d'un polynôme du second degré
  • $x_1$ et $x_2$ sont appelés les racines ou les zéros de $f$
 Les racines annulent le polynôme : $$f(x_1) = a \color{red}{(x_1 - x_1)} (x_1 - x2) = a \times \color{red}{0} \times (x_1 - x_2) = 0 $$ $$f(x_2) = a(x_2 - x_1) \color{blue}{(x_2 - x2)} = a \times (x_2 - x_1) \times \color{blue}{0} = 0 $$ Les fonctions suivantes définissent le même polynômes du second degré :
  • $f (x) = x^2 - 2x - 3$ (forme développée)
  • $g (x) = (x+1)(x-3)$ (forme factorisée)
Les racines de $f$ (et $g$) sont $-1$ et $3$. On développe $g (x) :$ $$ \begin{array}{ccl} g (x) &=& (x+1)(x-3) \\\\ &=& x^2 + x -3 x - 3 \\\\ &=& x^2 - 2 x - 3 \\\\ &=& f (x) \end{array} $$ Finalement, $f (x) = g (x)$ pour tout $x \in \mathbb{R}$ Attention, un polynôme du second degré n'a pas toujours une forme factorisée avec deux racines distinctes. Par exemple :
  • $f(x) = (x-1)^2$ a une racine double
  • $g(x) = x^2 + 1$ n'a pas de racine, et ne peut être factorisé

Racine double :

$f(x) = (x-1)\times(x-1)$ donc les deux racines sont la même valeur $1$.

On reconnaît une identité remarquable, et la forme développée de $f$ est $f(x)=x^2 - 2x + 1$

Pas de racine :

Si $g$ avait une forme factorisée, alors il aurait une racine (ou deux). Il existerait donc une valeur $x_1$ pour laquelle $g(x_1)=0$.

Or $g(x) = x^2 + 1 \geq 0 + 1 \geq 1$. Donc $g(x) \gt 0$ ne peut pas s'annuler.

Les racines $x_1$ et $x_2$ annulent le polynôme, c'est à dire : $$ f(x_1)=0 \text{ et } f(x_1)=0 $$ Inversement, si vous arrivez à deviner 2 valeurs qui annulent un polynôme du second degré, vous avez trouvé ses racines, et donc sa forme factorisée. Soit $f$ le polynôme du second degré défini par $f(x) = x^2 - 3x + 2$. On remarque que :
  • $f(1) = 1 - 3 + 2 = 0$ donc $1$ est une racine
  • $f(2) = 4 - 6 + 2 = 0$ donc $2$ est une racine
  • $a=1$
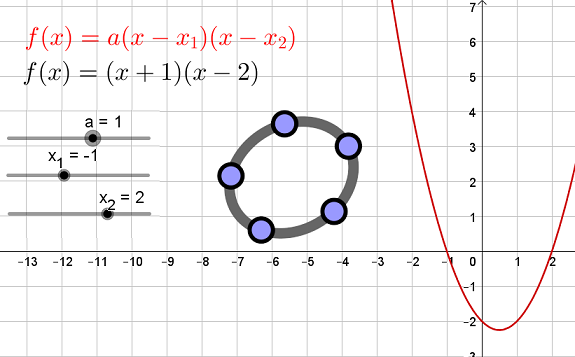
Donc la forme factorisée de $f$ est $f(x) = (x-1)(x-2)$ On peut visualiser sur l'animation ci-dessous les racines là où la courbe coupe l'axe des absisses :

Choisissez les racines du polynôme sur cette animation Geogebra...

Soit $f$ un polynôme du second degré ayant pour forme développée $f (x) = a x^2 + b x + c$ ($a, b, c$ des réels).

Alors, $f$ admet une forme canonique $f (x) = a (x - \alpha)^2 + \beta$ avec : $$ \alpha = \frac{-b}{2 a}$$ $$\beta = - \frac{b^2 - 4 a c}{4 a}$$

On suppose une forme canonique $f (x) = a (x - \alpha)^2 + \beta$. On développe : $$ f (x) = a (x - \alpha)^2 + \beta = a x^2 - 2 a \alpha x + \beta + a\alpha^2 $$ On identifie alors les coefficients de la forme développée : $$ \begin{array}{llll} b &=& - 2 a \alpha & \text{ (1)} \\\\ c &=& \beta + a \alpha^2 & \text{ (2)} \end{array} $$ Alors d'après (1), on isole alors $\alpha$ : $$ \alpha = \frac{b}{-2a} = \frac{-b}{2a} \text{ (3)} $$ Et d'après (2), on isole $\beta$ : $$ \begin{array}{llll} \beta &=& c - a \alpha^2 & \\\\ &=& c - a \frac{b^2}{4 a^2} & \text{ (d'apres (3))} \\\\ &=& \frac{4 a c - b^2}{4a} & \\\\ &=& - \frac{b^2 - 4 a c}{4 a} \end{array} $$ La démonstration précédente utilise une méthode générale qui consiste à faire apparaître le début d'une identité remarquable. Elle peut s'appliquer à n'importe quel exemple de polynôme du second degré. Il est possible de s'entraîner sur l'exerciseur suivant :

Des exemples générés aléatoirement et une correction automatique de la méthode.

La propriété précédente a deux intérêts :
  • Un intérêt pratique : passer de la forme développée à la forme canonique à l'aide d'une formule
  • un intérêt théorique : définir le discriminant (voir après) qui est fondamental pour le calcul de racines (donc très pratique)
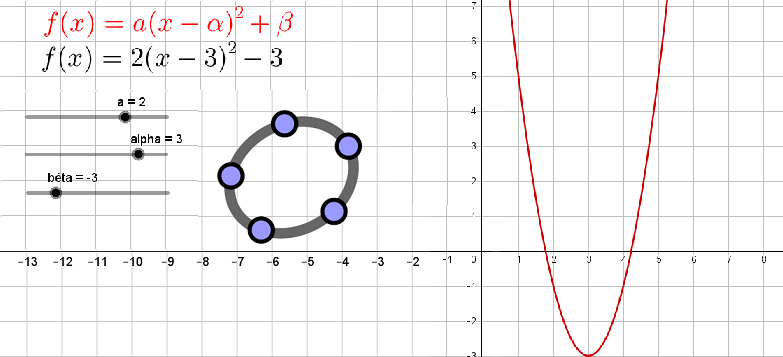
 On note $\Delta$ et on appelle discriminant le réel : $$ \Delta = b^2 - 4 a c $$ Ainsi, la forme canonique devient : $$ \begin{array}{lll} a^2 + b x + c &=& a (x - \alpha)^2 + \beta^2 \\\\ &=& a (x + \frac{b}{2 a})^2 - \frac{\Delta}{4 a} \end{array} $$ avec $\beta = - \frac{\Delta}{4 a} $ On peut visualiser sur l'animation ci-dessous l'influence des coefficients $\alpha$ et $\beta$ sur la courbe :

Choisissez les racines du polynôme sur cette animation Geogebra...

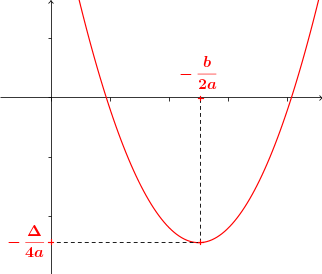
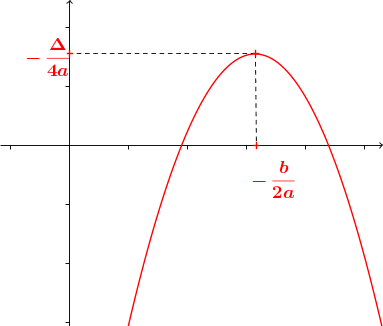
La forme canonique permet de préciser le tableau de variation d'un polynôme du second degré : La parabole représentant le trinôme $f$ est symétrique par rapport à la droite d'équation $x = \frac{-b}{2a}$ et son sommet a pour coordonnées $(\frac{-b}{2a};-\frac{\Delta}{4a})$ :
Cas $a \gt 0$ : Cas $a \lt 0$ :
$$ \begin{array}{c|lcccr|} x &-\infty & & -\frac{b}{2a} & & +\infty\\\\\hline f (x) & & \searrow & -\frac{\Delta}{4a} & \nearrow & \\\\ \end{array} $$ $$ \begin{array}{c|lcccr|} x &-\infty & & -\frac{b}{2a} & & +\infty\\\\\hline f (x) & & \nearrow & -\frac{\Delta}{4a} & \searrow & \\\\ \end{array} $$

Idée de preuve pour l'extremum (cas $a$ positif)

Pour bien comprendre les variations d'un polynôme du second degré, il est nécessaire de s'intéresser à sa forme canonique : $$ f (x) = a (x - \alpha)^2 + \beta^2 $$

Comme un carré est toujours positif, et que $a \gt 0$, l'expression $a (x - \alpha)^2$ est positive pour tout $x$ réel

Cette remarque a deux conséquences :

  • La valeur la plus basse est atteinte quand $(x - \alpha)^2$ s'annule. Ainsi, l'abscisse du sommet vaut $\alpha = -\frac{b}{2a}$ (et on retrouve facilement l'ordonnée en calculant $f (\alpha)$).
  • Lorsque $x$ s'éloigne de $\alpha$ la valeur de $(x - \alpha)^2$ grandit, ce qui explique les variations.

Preuve formelle :

On démontre qu'un extremum est atteint en $x=\alpha=-\frac{b}{a}$ :
Cas $a \gt 0$ :
$$ \begin{array}{llll} & & (x - \alpha)^2 \geq 0 & \\ &\Rightarrow & a (x - \alpha)^2 \geq 0 & \text{ car } a\gt 0 \\ &\Rightarrow & a (x - \alpha)^2 + \beta \geq \beta & \\ &f(x) \geq \beta & \\ \end{array} $$ Or, $f(\alpha) = \beta$, donc $f$ atteint son minimum $\beta$ en $x=\alpha=-\frac{b}{a}$
Cas $a \lt 0$ :
Le raisonnement est le même : $$ \begin{array}{llll} & & (x - \alpha)^2 \geq 0 & \\ &\Rightarrow & a (x - \alpha)^2 \leq 0 & \text{ car } a\lt 0 \\ &\Rightarrow & a (x - \alpha)^2 + \beta \leq \beta & \\ &f(x) \leq \beta & \\ \end{array} $$ Or, $f(\alpha) = \beta$, donc $f$ atteint son maximum $\beta$ en $x=\alpha=-\frac{b}{a}$

Symétrie de la courbe

Si l'on prend deux points d'absisses $x_1=\alpha - d$ et $x_2=\alpha + d$ à égale distance de $\alpha$, ils auront la même ordonnée.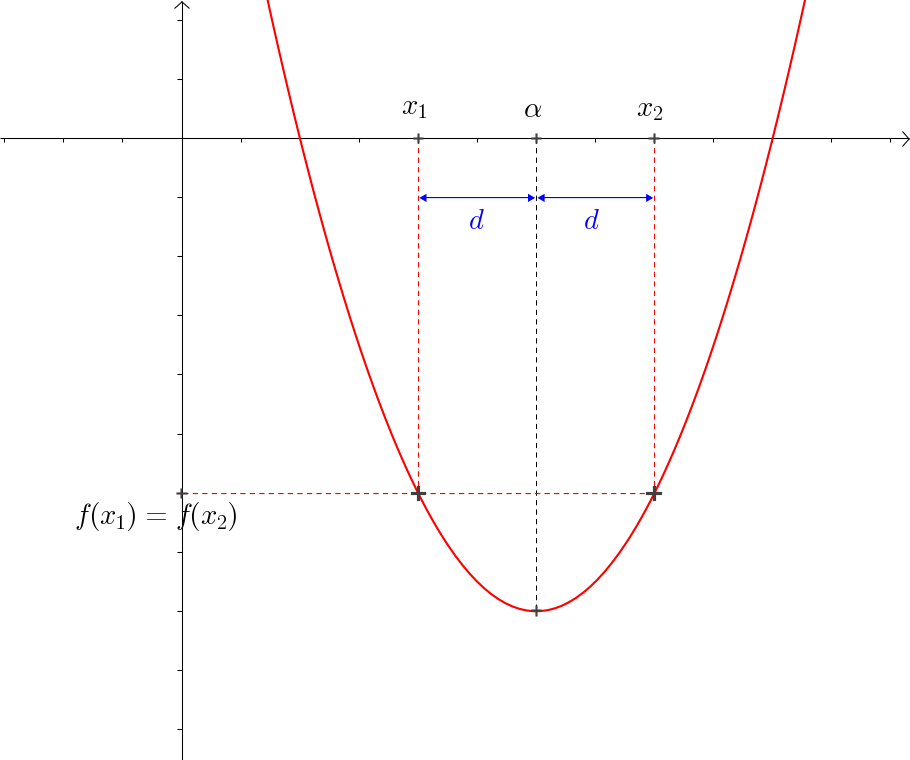 Vérifions par le calcul : $$ \begin{array}{lll} f (x_1) = a (x_1 - \alpha)^2 + \beta = a (\alpha - d - \alpha)^2 + \beta = a \times (-d)^2 + \beta = & a d + \beta \end{array} $$ Et de même : $$ \begin{array}{lll} f (x_2) = a (x_2 - \alpha)^2 + \beta = a (\alpha + d - \alpha)^2 + \beta = & a d + \beta = f (x_1) \end{array} $$

La suite de ce chapitre s'intéressera aux racines d'un polynôme du second degré...