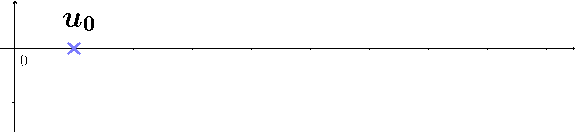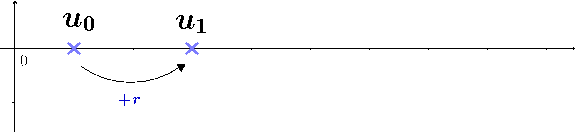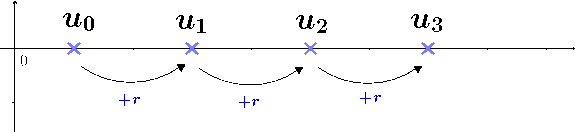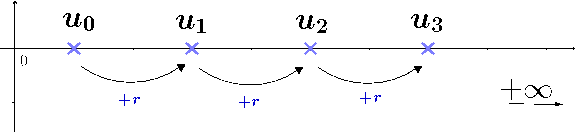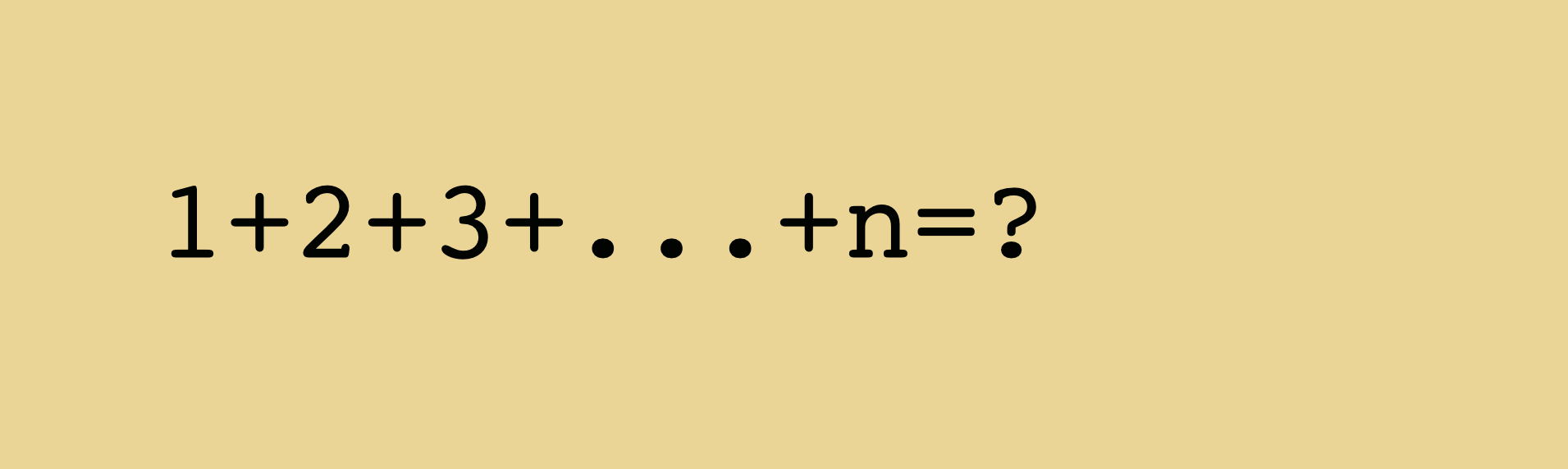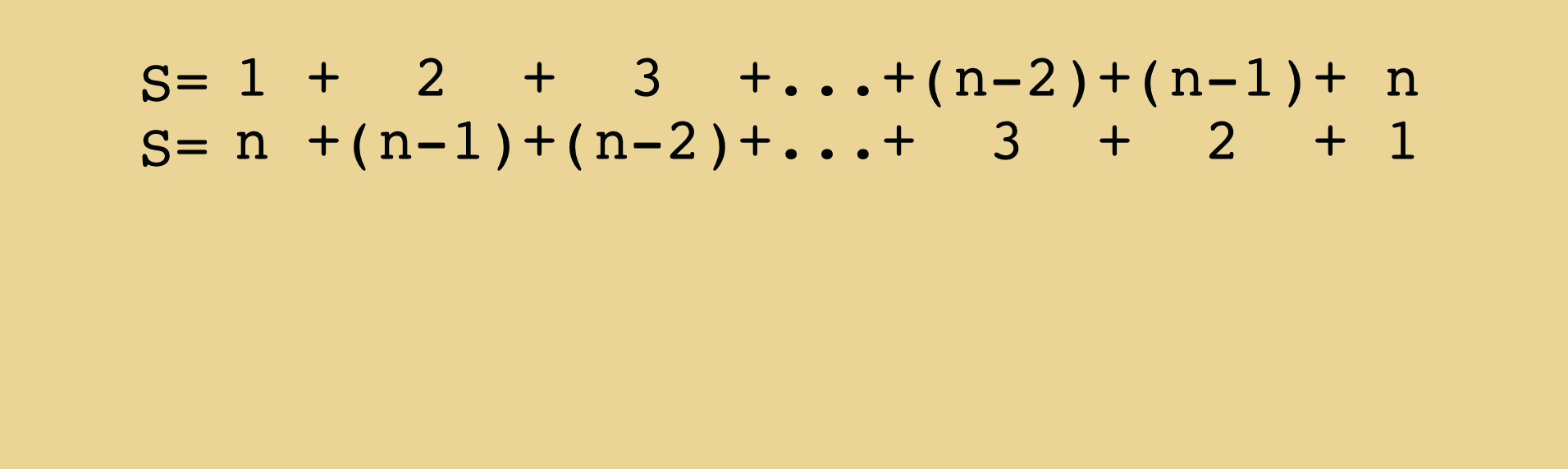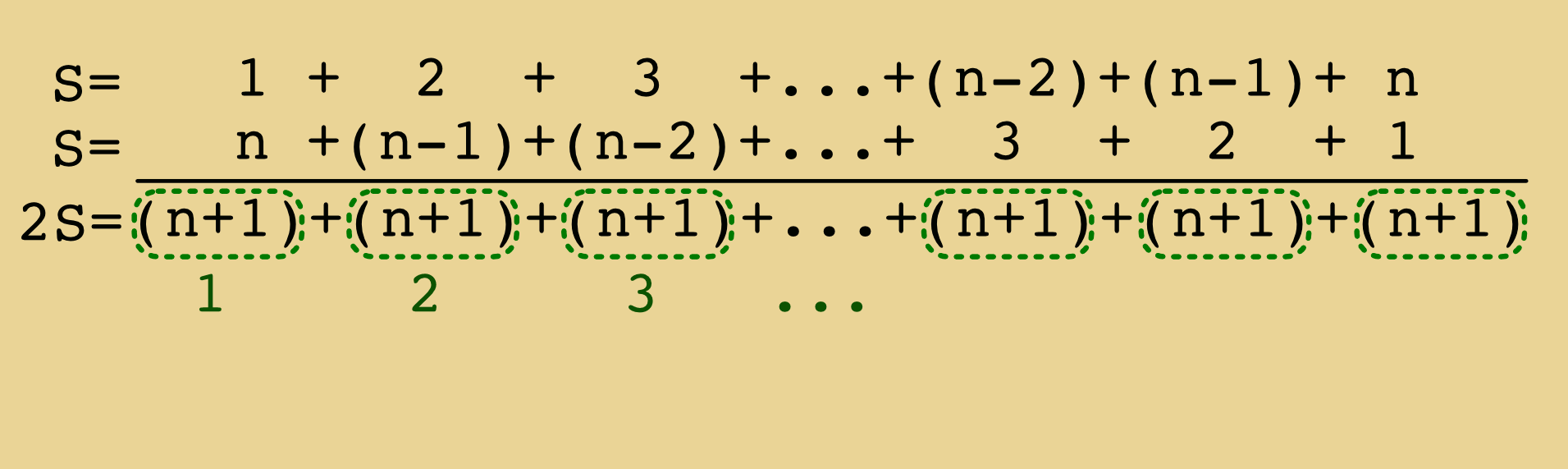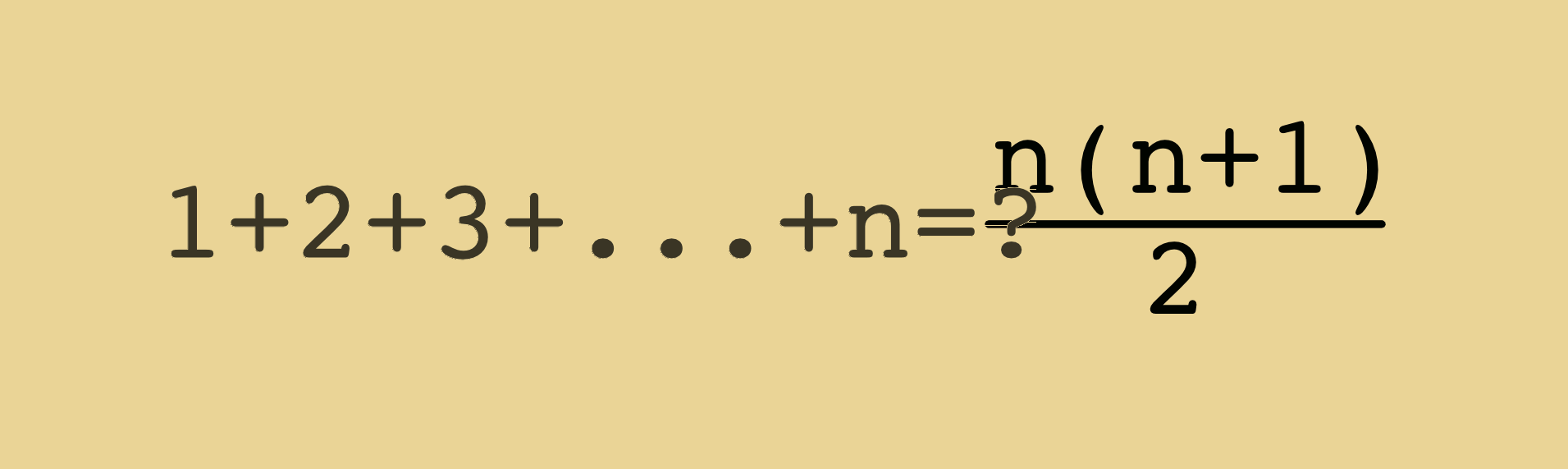Suites arithmétiques

Précédemment, nous avons découvert les suites numériques. Nous avons vu qu'elle pouvait modéliserOn dit qu'une suite modélise une situation quand les valeurs calculées par sa formule mathématique sont proches des observations numériques réelles et peuvent par exemple servir à tenter des prédiction comme en météorologie. des phénomènes réels.

Nous avions appris qu'une suite peut être définie de deux manières différentes : par une formule explicite ou une formule de récurrence.

  • La formule de récurrence permet de calculer le terme suivant $u_{n+1}$ à partir de l'actuel $u_n$. Elle n'est souvent que le point de départ d'un modèle.
  • La formule explicite permet de calculer le $n$-ième terme $u_n$ directement sans passer par tous les précédents. C'est la plus pratique des deux.
  • Malheureusement, la formule explicite d'une suite n'est pas toujours évidente ou simple à trouver.
 Si vous avez besoin de plus de rappels, vous pouvez relire le cours précédent : test Introduction aux suites numériques. Formules explicite et récurrente. Dans cette partie, nous n'étudierons qu'un seul type de suites : les suites arithmétiques. Elles peuvent être définie par récurrence mais aussi de manière explicite. Chacune de ses valeurs d'obtient en ajoutant la même valeur $r$ à la précédente. Le nombre $r$ s'appelle la raison de la suite.
Une suite de valeurs observée a une progression arithmétique si pour passer d'un terme au suivant, on lui ajoute une valeur fixée (la raison). Mathématiquement celà se définit de la manière suivante : Une suite $(u_n)$ est arithmétique de raison $r$ si elle est définie par la formule de récurrence : $$ \left\{ \begin{array}{ccc} u_{n+1} &=& u_{n} + r \\ u_0 &=& \text{terme initial} \end{array} \right. $$

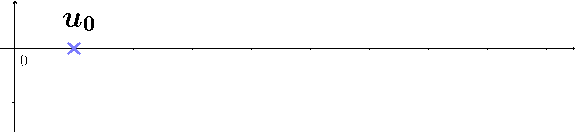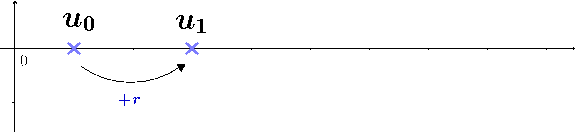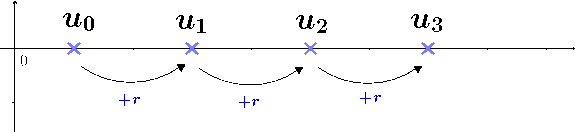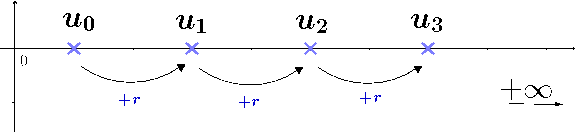
La suite des nombre pair $ (P_n) = (0,2,4,6,8,10,...)$ a une progression arithmétique car elle augmente de $2$ entre chaque terme.

Le $(n+1)$-ième terme $P_{n+1}$ est égal au précédent auquel on ajoute $2$, c'est à dire $P_{n} + 2$. On a la formule de récurrence suivante : $$ \left\{ \begin{array}{ccc} P_{n+1} &=& P_{n} + 2 \\ P_0 &=& 0 \end{array} \right. $$ La suite des nombres pairs n'est rien d'autre que la suite arithmétique de raison $r=2$ et de premier terme $0$.

La suite des nombre impairs $ (I_n) = (1,3,5,7,9,11,...)$ a une progression arithmétique car elle augmente de $2$ entre chaque terme.

Comme pour les nombres pairs, le $(n+1)$-ième terme $I_{n+1}$ est égal à $I_{n} + 2$. On a la formule de récurrence suivante : $$ \left\{ \begin{array}{ccc} I_{n+1} &=& I_{n} + 2 \\ I_0 &=& 1 \end{array} \right. $$ En changeant seulement la valeur initiale, on obtient une suite très différente.

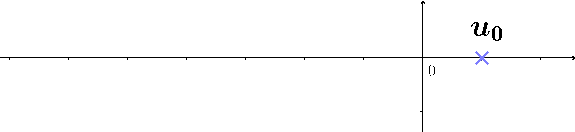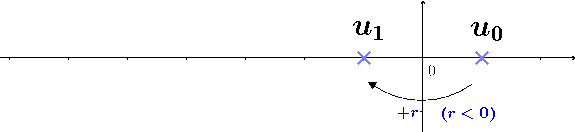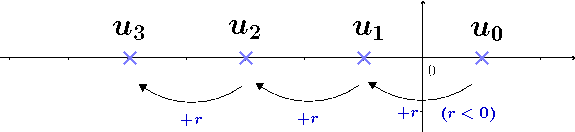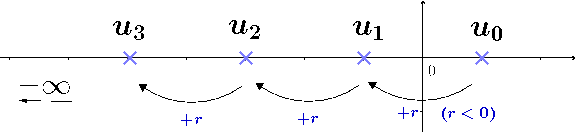
La suite des puissances de $2$ : $(P_n) = (1,2,4,8,16,...)$ n'est pas arithmétique. En effet, la différence entre deux termes consécutifs n'est pas toujours la même : $$ \left\{ \begin{array}{ccc} P_{2} &=& P_{1} + 1 \\ P_3 &=& P_2 + 2 \end{array} \right. $$ Or, $2\neq1$ donc, la suite n'est pas arithmétique. La formule de récurrence permet de calculer les termes dans l'ordre à partir du premier. La propriété suivante donne une formule explicite permettant le calcul de termes d'indices arbitraires: Soit $(u_n)$ une suite arithmétique de raison $r$ et de terme initial $u_0$. Pour tout entier $n$, on a : $$ u_n = u_0 + n r $$

Dans la formule par récurrence, si on doit partir de $u_0$ ajoutera $r$ autant de fois qu'il faut pour arriver jusqu'à $u_n$

Dans la formule explicite, on ajoute directement $n\times r$ au premier terme $u_0$ pour faire les $n$ étapes en une seule :

Ce qui donne : $$ \begin{array}{ccc} u_{1} &=& u_{0} + r \\ u_{2} &=& u_{0} + 2r \\ u_{3} &=& u_{0} + 3r \\ &...& \\ u_{n} &=& u_{0} + n r \\ \end{array} $$ La suite des nombres pairs $(P_n)$ est définie explicitement par : $$ u_n = 2 n$$ On peut ainsi calculer n'importe quelle valeur directement : $$ \begin{array}{ccccc} u_{0} &=& 2\times 0 &=& 0\\ u_{1} &=& 2\times 1 &=& 2\\ u_{2} &=& 2\times 2 &=& 4\\ u_{1000} &=& 2\times 1000 &=& 2000\\ \end{array} $$ Le $1000$-ème nombre pair est $2000$ ! De même, La suite des nombres impairs $(I_n)$ est définie explicitement par : $$ u_n = 2 n + 1$$ Et donc, on est heureux d'apprendre que le 1000ème nombre impair est $2\times1000+1 = 2001$ ! Ces exemples sont très simples. Parfois les suites arithmétiques sont un peu plus complexes (jamais vraiment, ce sont des suites assez basiquesNon, je n'ai mis aucun gif ici ! Un peu trop évident...)...

Afin de démontrer qu'une suite $(u_n)$ est arithmétique, il faut montrer qu'il existe un nombre réel $r$ tel que $u_{n+1} = u_n + r$.

Pour cela, on calcule $u_{n+1} - u_n$ et après simplification on doit obtenir un nombre réel. La suite est alors arithmétique et ce nombre est la raison $r$.

Afin de démontrer qu'une suite $(u_n)$ n'est pas arithmétique, il suffit de trouver des contre-exemples, c'est à dire trouver un entier $k$ tel que : $$ u_{k+1} - u_{k} \neq u_{k+2} - u_{k+1} $$

Soit $(a_n)$ et $(b_n)$ deux suites définie par : $$ \begin{array}{cccc} a_n = (n-2)^2 & \text{ et } & b_n=(n+1)^2 \end{array} n\in\mathbb{N} $$ Montrer que les suites $(a_n)$ et $(b_n)$ ne sont pas arithmétiques Pour tout $n\in\mathbb{N}$, on définit la suite $(u_n)$ par $$ u_n = a_n - b_n $$ Démontrer que $(u_n)$ est arithmétique. Préciser son premier terme $u_0$ et sa raison $r$. On calcule les trois premiers termes de $(a_n)$ : $$ \begin{array}{ccc} a_0&=& (0 - 2)^0 = 1 \\ a_1&=& (1 - 2)^1 = -1 \\ a_2&=& (2 - 2)^2 = 0 \\ \end{array} $$ Si (a_n) était arithmétique on aurait une raison $r$ telle que $a_1 - a_0$ = $a_2 - a_1$. Or $a_1 - a_0 = -2$ et $a_2 - a_1 = 1$. La suite $(a_n)$ n'est pas arithmétique. On calcule les trois premiers termes de $(b_n)$ : $$ \begin{array}{ccc} b_0&=& (0 + 1)^0 = 1 \\ b_1&=& (1 + 1)^1 = 2\\ b_2&=& (2 + 1)^2 = 9 \\ \end{array} $$ De même on a $b_1 - b_0 = 1$ et $b_2 - b_1 = $. La suite $(b_n)$ n'est pas arithmétique. Soit $n\in\mathbb{N}$. On calcule $u_{n+1} - u_n$ : \begin{array}{ccl} u_{n+1} - u_n &=& a_{\color{red}{n+1}} - b_{\color{red}{n+1}} - (a_\color{blue}{n}-b_\color{blue}{n}) \\ &=& (\color{red}{n+1} - 2)^2 - (\color{red}{n+1} + 1) - \left((\color{blue}{n} - 2)^2 - (\color{blue}{n}+1)^2\right) \\ &=& (n-1)^2 - (n+2)^2 - (n-2)^2 + (n+1)^2\\ &=& n^2-2n+1 - (n^2+4n+4) - (n^2-4n+4) + (n+2n+1)\\ &=& n^2-2n+1 - n^2-4n-4 - n^2+4n-4 + n^2+2n+1\\ u_{n+1} - u_n &=& -6\\ \end{array} De plus $u_0 = a_0 - b_0 = 4-1=3$. Donc $(u_n)$ est une suite arithmétique de premier terme $u_0 = 3$ et de raison $r=-6$
Une suite arithmétique est croissante ou décroissante, ça dépendra du signe de la raison $r$ : On considère une suite arithmétique $(u_n)$ de raison $r$ et de premier terme $u_0$ :
  • Si $r > 0$, alors la suite est croissante.
  • Si $r < 0$, alors la suite est décroissante
Et donc si $r=0$, la suite est constante et vaut toujours $u_0$ C'est assez intuitif, mais on peut le démontrer en étudiant le signe de $u_{n+1} - u_{n}$ où $n\in\mathbb{N}$ : \begin{array}{ccll} u_{\color{red}{n+1}} - u_{\color{blue}{n}} &=& u_0 + \color{red}{(n+1)}r - \left(u_0 + \color{blue}{n}r\right) & \text{ (formule explicite)} \\ &=& u_0 + \color{red}{nr+r} - u_0 - \color{blue}{n}r & \\ &=& r & \\ \end{array} Donc $u_{n+1} - u_{n} = r$ est du signe de $r$. Si $r$ est positif, la suite est croissante. Si $r$ est négatif, elle est décroissante. Dans cet exemple, $q > 1$ ($q=2$) et $u_0 > 0$ la suite est croissante : Dans cet exemple, $q < 1$ ($q=\frac{1}{2}$) et $u_0 > 0$ la suite est décroissante : La représentation graphique d'une suite arithmétique définie pour tout $n$ entier par $u_n=u_0+rn$ est un nuage de points appartenant la droite d'équation affine $y=rx+u_0$ : On vérifie que le sens de variation dépend bien du signe de la raison $r$.
Soit $n$ un entier naturel : $$ 1 + 2 + 3 + ... + n = \frac{n (n+1)}{2} $$ Soit $n \in \mathbb{N}$, on définit la suite $S_n$ comme la somme des $n$ premiers entiers non nuls : $$ S_n = 1+2+3+...+n $$ On peut aussi écrire cette somme "à rebours": $$ S_n = n+(n-1)+(n-2)+...+ 2 + 1 $$ Pour calculer $S_n$, on va d'abord calculer le double en additionant les deux formules précédentes : $$ \begin{array}{cccccccccccc} 2 S_n &=& & 1 &+& 2 &+& 3 &+& ... &+& n \\ & & + & n &+& (n-1) &+& (n-2) &+& ... &+& 1 \\ \hline 2 S_n &=& & (n+1) &+& (n+1) &+& (n+1)&+& ... &+& (n+1) \\ \end{array} $$ La somme de $(n+1)$ est répétée $n$ fois, donc : $$ \begin{array}{ccl} 2 S_n &=& n\times (n+1)\\ S_n &=& \frac{n (n+1)}{2} \end{array} $$ Ainsi, on peut calculer la somme des 100 premiers entiers rapidement : $$ 1+2+3+...+100 = \frac{100\times 101}{2} = \frac{10100}{2} = 5050 $$
Très bientôt nous découvrirons un nouveau type de suites ...