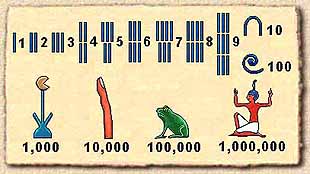
- Comprendre le concept de base de représentation
- Passer d'une base à une autre
- Maîtriser le binaire et l'hexadécimal
A cette époque, une partie sur une borne coûtait une petite pièce, laquelle pouvait offrir le privilège de jouer sans limite jusqu'au Game Over. Encore fallait-il être habile car la difficulté augmentait vite. Il existait (et existe toujours) de véritables champions du high score, en rivalisant pour conquérir les places hautes du Hall of Fame de leurs jeux préférés.
C'est pour cette raison qu'à cette époque, les jeux d'arcade n'ont pas de fin. Les niveaux ne sont souvent que des copies des précédents avec davantage d'ennemis, de vitesse, etc.
Un de ces jeux, le très populaire Pac-Man a pourtant une fin. Une fin assez inattendue, qui se produit lorsque le joueur atteint le 
-ème niveau. Cet écran complètement "glitché" s'appelle le Kill Screen :
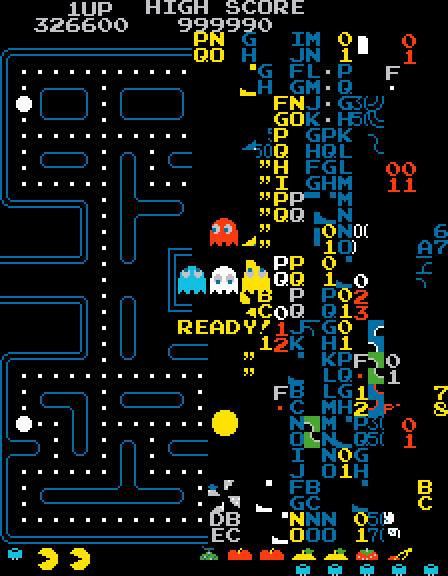Et comme chacun sait, $256 = 2^8$. Coïncidence ? Pas du tout ! Nous découvrirons dans ce cours les raisons de ce bug en comprenant comment sont codés les nombres, ce qu'est un bit ainsi qu'un octet.
La représentation graphique d'un chiffre en base dix est une convention, on pourrait lui préférer n'importe quelle autre sans changer le système numérique. Voici quelques autres exemples existants :
| Valeur | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Arabe oriental | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Bengalais | ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ |
| Braille | ⠚ | ⠁ | ⠃ | ⠉ | ⠙ | ⠑ | ⠋ | ⠛ | ⠓ | ⠊ |
| Devanagari | ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ |
| Gujarati | ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ |
| Gurmukhi | ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ |
| Kannada | ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ |
| Khmer | ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ |
| Laotien | ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ |
| Malayalam | ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ |
| Myanmar | ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ |
| N'ko | ߀ | ߁ | ߂ | ߃ | ߄ | ߅ | ߆ | ߇ | ߈ | ߉ |
| Oriya | ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ |
| Osmanya | 𐒠 | 𐒡 | 𐒢 | 𐒣 | 𐒤 | 𐒥 | 𐒦 | 𐒧 | 𐒨 | 𐒩 |
| Persan/Ourdou | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
| Tamoul | ௦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ |
| Télougou | ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ |
| Thaï | ๐ | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ |
| Tibétain | ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ |
| Pac-Man |  |
 |
 |
 |
|
 |
|
 |
|
 |
... mais on pourrait tout à fait imaginer des systèmes très différents en choisissant pour certaines raisons une autre base !
dans plusieurs bases :
On compte 1 dizaine de pièces.
Ce que nous écrivons $\color{red}{2}\color{blue}{6}$
se note :
$$
{\Huge \overline{\color{red}{2}\color{blue}{6}} ^ {\large 10}}
$$
On compte 1 cinquaine de pièces.
On compte 2 cinquaines de pièces
1 vingt-cinquaine, 0 cinquaine et 1 pièces
Ce que nous écrivons $\color{green}{1}\color{red}{0}\color{blue}{1}$ pièces
se note :
$$
{\Huge \overline{\color{green}{1} \color{red}{0} \color{blue}{1} } ^ {\large 5}}
$$
1 paire de pièces
1 quatraine de pièces
1 huitaine de pièces
1 seizaine de pièces
1 seizaine et 1 huitaine de pièces
Ce que nous écrivons $\color{purple}{1}\color{orange}{1}\color{green}{0}\color{red}{1}\color{blue}{0}$ pièces
se note :
$$
{\Huge \overline{\color{purple}{1}\color{orange}{1}\color{green}{0}\color{red}{1}\color{blue}{0}} ^ {\large 2}}
$$
peut se noter :
$$
{ \Large \overline{26} ^ {\normalsize 10} = \overline{101} ^ {\normalsize 5} = \overline{11010}^{\normalsize 2}}
$$
peut se noter :
$$
{ \Large \overline{26} ^ {\normalsize 10} = \overline{101} ^ {\normalsize 5} = \overline{11010}^{\normalsize 2}}
$$
(quand on ne précise pas la base, par défaut il s'agit de la base décimale)
- Les positions d'un chiffre dans un nombre binaire s'appellent des bits.
- Un octet vaut 8 bits.
- Le 4ème bit de $\overline{1010}^2$ vaut $1$.
- Il faut 5 bits pour écrire en binaire le nombre $16 = \overline{10000}^2$
- Avec $3$ bits on peut représenter $8$ nombres (de 0 à 7)
- Avec $1$ octet on peut représenter $512$ nombres (de 0 à $\overline{1111\ 1111}^2 = 511$)
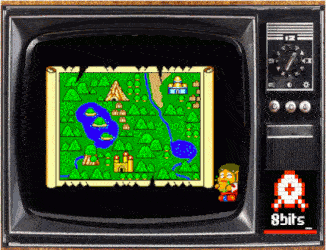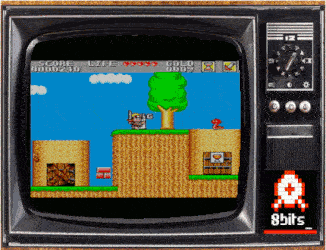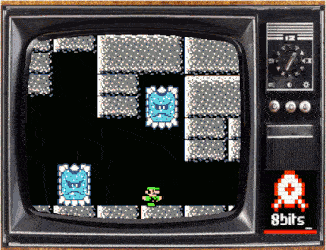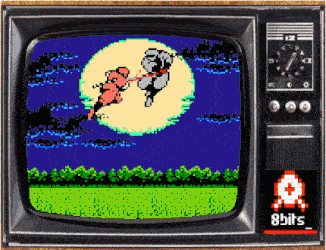
La conséquence la plus évidente de cette progression est visuelle : nombre de couleurs, taille et nombre de sprites
Bien sûr, cette phase exponentielle ne peut pas durer indéfiniment. Il n'existe pas d'ordinateur commercialisé dont le processeur traite des données en 128 bits. Si vous voulez en apprende davantage sur la loi de Moore dans le jeu vidéo :
- $b_i$ représente le $i$-ème bit du nombre $b$ en binaire.
- $b_i = 0$ ou $1$, pour $i$ allant de $0$ à $n-1$
- $b_0$ est appelé le bit de poids faible (le plus à droite)
- $b_{n-1}$ est appelé le bit de poids fort (le plus à gauche)
- On cherche la puissance de $2$ la plus proche de $\color{blue}{61}$ par valeur inférieure, c'est $2^5 = \color{brown}{32}$.
- On retire cette puissance à notre nombre, et il reste une valeur $r_0$ : $61 = \color{brown}{32} + r_0 = \color{red}{32} + 29 $ à
- On réitère la même opération avec $r_0=29$. La puissance la plus proche est $\color{purple}{16}$.
- Et donc $29 = \color{purple}{16} + r_1 = \color{purple}{16} + 13 $
- Et ainsi de suite avec des puissances de plus en plus petites : $$ \begin{array}{ccc} 61 &=& \color{brown}{32} &+& \color{purple}{16} &+& \color{orange}{8} &+& \color{green}{4} &+& \color{red}{0} &+& \color{blue}{1} \\ &=& \color{brown}{1 \times 2^5} &+& \color{purple}{1 \times 2^4} &+& \color{orange}{1 \times 2^3} &+& \color{green}{1 \times 2^2} &+& \color{red}{0 \times 2^1} &+& \color{blue}{1 \times 2^0} \\ \end{array} $$
- La décomposition nous permet de dire que $$ \overline{61}^{10} = \overline{\color{brown}{1}\color{purple}{1}\color{orange}{1}\color{green}{1}\color{red}{0}\color{blue}{1}}^{2} $$
Cette méthode, plus directe repose sur des divisions entières successives par $2$.
- On commence avec le nombre en base 10
- On le divise par 2 et on retient le reste (qui vaut 1 ou 0)
- On recommence avec le quotient précédent et on retient le reste
- On s'arrête quand le quotient est nul
- Le nombre binaire est formé des restes (le dernier est le bit de poids fort, il faut lire à du haut vers le bas)
Pour l'utilisateur et l'informaticien, cette base est un peu pénible. Ses nombres sont très longs à écrire et on a tendance à traiter des informations plus grandes qu'un bit (d'où l'utilisation des octets vu avant).
La base 10 est trop éloignée de l'architecture d'un ordinateur. Les bases satisfaisantes sont des puissances de 2. Le système le plus utilisé en informatique est l'hexadécimal, c'est à dire la base 16. Pour représenter 16 chiffres différents, on utilise les lettres de l'alphabet au delà de 9. $$ \begin{array}{r|r} \text{base } 2 & \text{base } 10 & \text{hex} \\ \hline 0 & 0 & 0\\ 1 & 1 & 1\\ 1\ 0 & 2 & 2\\ 1\ 1 & 3 & 3\\ 1\ 0\ 0 & 4 & 4\\ 1\ 0\ 1 & 5 & 5\\ 1\ 1\ 0 & 6 & 6\\ 1\ 1\ 1 & 7 & 7\\ 1\ 0\ 0\ 0 & 8 & 8\\ 1\ 0\ 0\ 1 & 9 & 9\\ 1\ 0\ 1\ 0 & 10 & A\\ 1\ 0\ 1\ 1 & 11 & B\\ 1\ 1\ 0\ 0 & 12 & C\\ 1\ 1\ 0\ 1 & 13 & D\\ 1\ 1\ 1\ 0 & 14 & E\\ 1\ 1\ 1\ 1 & 15 & F\\ \dots & \dots \\ \end{array} $$
- Réunir par paquets de 4 bits le nombre binaire à partir du poids faible
- Remplacer chaque paquet de 4 par l'équivalent en hexadécimal (dans la table ci-dessus)
- On le regroupe par paquets de 4 bits : $\color{blue}{0 0 1 1} \ \ \color{red}{1 1 0 0}$
- On remplace par les chiffres hexadécimaux correspondants : $ \color{blue}{3} \color{red}{C} $
- Et donc : $$\overline{1 1 1 1 0 0}^2 = \overline{3C}^{hex}$$
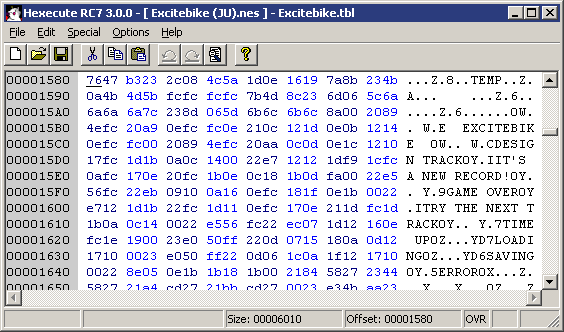Ci-dessus un vieux jeu vidéo est édité. Les données textuelles sont décodées à droite (un caractère tient sur un octet).
- $h_i$ représente le chiffre du $i$-ème rang du nombre $h$ en hexadécimal.
- $h_i \in \{0,1,2,...,F\}$, pour $i$ allant de $0$ à $n-1$
Cette méthode repose également sur des divisions entières successives, mais par $16$.
- On commence avec le nombre en base 10
- On le divise par 16 et on retient le reste (entre 0 et 15)
- On recommence avec le quotient précédent et on retient le reste
- On s'arrête quand le quotient est nul
- Le nombre hexadécimal est formé des restes (le dernier est le bit de poids fort, il faut lire à du haut vers le bas)
Nous comprenons maintenant que l'indice du niveau de Pac-Man était sans doute codé sur un octet ne permettant de compter que jusqu'à 255. La vidéo ci-dessous (en anglais) va dans les détails (plutôt techniques) de ce fameux fill-screen :
Il y a énormément à dire sur la représentation des nombres. Le binaire et l'hexadécimal reviendront plus tard dans l'année, entre autre pour comprendre la représentation des couleurs en CSS (chapitre web) mais également les adresses IP dans le chapitre consacré aux réseaux.
