Fonction exponentielle
On entend souvent parler de croissance exponentielle dans les médias. Ce qui est, à raison, synonyme d'une très forte croissance. Pour être plus précis un phénomène suit une croissance exponentielle lorsque le taux de croissance est constant. Une quantité qui est multipliée par une même valeur chaque année suit une croissance exponentielle. Le premier exemple naturel auquel on peut penser est l'étude d'une population. En effet, selon un modèle simple, le nombre d'individus de la nouvelle génération est obtenu en multipliant par le taux d'accroissementCe taux, considéré constant sur des périodes relativement courtes, est égal à la différence entre le taux de natalité et le taux de mortalité de nombre d'individus de la population précédente. Nous connaissons déjà ce type de phénomènes étudiés dans le chapitre sur les suites. Si on note $p_n$ la population de l'a $n$-ième génération et $t$ le taux d'accroissement, l'évolution de la population suit la formule : $$ p_{n+1} = t \times p_n $$ Les suites géométriques décrivent des phénomènes à croissance exponentielle. Thomas Malthus fut un des premier à s'intéresser mathématiquement à la population de l'Angleterre (à faire de la démographie...) et à confronter la croissance exponentielle de la population à la croissance affine des ressources ! 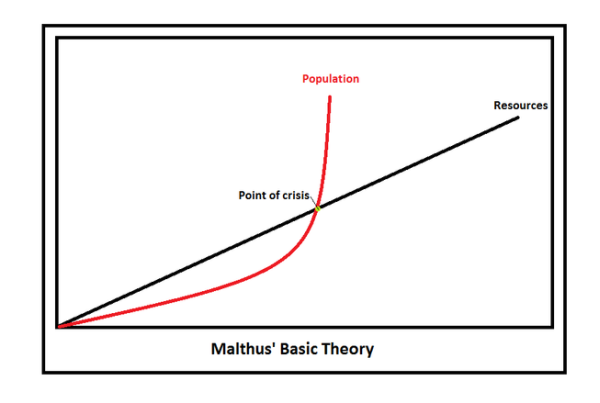Sa théorie présentait des failles théoriquesNotamment elle ne tenait pas compte de la révolution industrielle augmentant la production des ressources, ni la baisse du taux de natalité à venir. , mais énonçait pour la premier fois cette idée simple selon laquelle lorsque la production de ressources est dépassée par une trop forte démographie, des crises graves surviennent. On appelle catastrophe Malthusienne en "hommage" à Thomas Malthus, un effondrement de la démographie suite à une croissance exponentielle de la population. Les exemples avérés et documentés sont assez rares, sauf pour quelques systèmes isolés. Les rennes de l'île de Saint Matthieu est un exemple du 20ème siècle, présenté par ce web-comic de Stuat Mc-Millen. Les phénomènes à croissance exponentielle sont nombreux et pour n'en citer que quelques-uns :

La réaction en chaîne nucléaire

La loi de Moore (puissance de calcul des ordinateurs)

La propagation des rumeurs sur internet

La reproduction des bactéries

Le monde actuel est en accélération à tous les niveaux : crises économiques, écologiques, climatiques, productivisme accru, ... La collapsologieLa collapsologie n'est pas une discipline scientifique à proprement parler. Il s'agit plutôt d'un exercice interdisciplinaire tentant de prévoir les effets de la fin de l'ère industrielle et de ce qui la suivra. Elle est critiquée pour sa vision pessimiste et est à ce titre comparée à un malthusianisme moderne. tente d'en faire une synthèse "scientifique". Nous sommes maintenant entré dans une ère de la croissance exponentielle généralisée. Il est important d'en appréhender les mécaniques et les implications concrètes.
On a passé en revue un certain nombre d'exemples ayant en commun un taux d'évolution constant : $$ \frac{p_{n+1} - p_{n}}{p_n} = constante $$ Nous cherchons une fonction permettant de décrire théoriquement ces phénomènes. Du point de vue d'une fonction, ce taux d'évolution constant se traduirait par une dérivée égale à elle même. $$ \frac{f'(x)}{f(x)} = constante $$ La question est donc posée : existe-il une fonction dont la dérivée croît à la même vitesse qu'elle même ? La réponse est le point de départ de ce cours : Il existe une unique fonction $f$ définie sur $\mathbb{R}$ dérivable telle que : $$ \left\{ \begin{array}{clll} f(x) &=& f'(x) & \text{pour tout } x \in \mathbb{R} \\ f(0) &=& 1 \end{array} \right. $$ L'existence est admiseUn résultat mathématique est dit admis lorsqu'on l'accepte comme vrai sans preuve. Celà ne signifie pas que la preuve n'existe pas, mais qu'elle est trop compliquée ou fait appel à des notions hors du programme de terminale.. Seule l'unicité est démontrée en terminale.

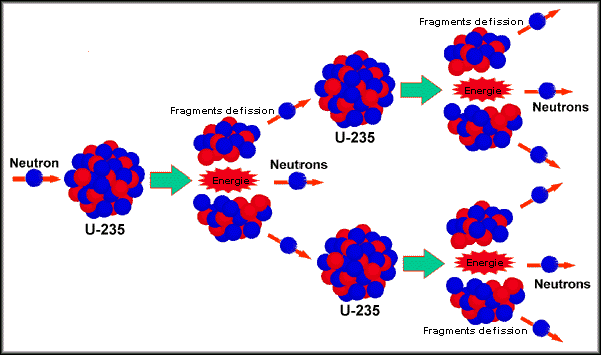
Raisonnement :

Pour démontrer l'unicité, on montre en fait qu'il ne peut pas exister deux fonctions vérifiant les propriétés. Pour celà, on supposera que si il en existe deux, $f$ et $g$, alors $f=g$.

Organisation de la preuve :

  1. fonction non-nulle : On aura besoin d'utiliser le fait que les fonctions $f$ ou $g$ ne peuvent pas s'annuler.
  2. unicité de la fonction: on va démontrer que $\frac{f(x)}{g(x)}=1$ pour tout $x\in\mathbb{R}$
La première partie de la preuve est ce qu'on appelle un lemme, c'est à dire un résultat préliminaire, utile à un résultat plus important. Il est donc possible de commencer par la deuxième partie concernant l'unicité en revenant par la suite sur le lemme.

Preuve :

Soit $f$ une fonction vérifiant les hypothèses du théorème, c'est à dire :
  • $f$ définie et dérivable sur $\mathbb{R}$
  • $\color{red}{f'=f}$
  • $\color{blue}{f(0)=1}$.
On définit la fonction $k$ par $k(x) = f(x)f(-x)$ pour tout $x\in\mathbb{R}$.

L'objectif est de démontrer que la fonction $k$ ne s'annule pas ce qui implique que $f$ ne s'annule pas non plus.

La fonction $k$ est dérivable sur $\mathbb{R}$ : $$ \begin{array}{clll} k'(x) &=& f'(x)f(-x)+ f(x)\times (-1)\times f'(-x) & \text{car } [f(ax+b)]'=a f'(ax+b)\\ k'(x) &=& f'(x)f(-x)- f(x)\times f'(-x) & \\ k'(x) &=& f(x)f(-x)- f(x)\times f(-x) & \text{car } \color{red}{f' = f} \\ k'(x) &=& 0& \\ \end{array} $$ Donc la fonction $k$ est constante car sa dérivée est nulle. On calcule sa valeur : $$ k(0) = \color{blue}{f(0)f(0) = 1\times 1} = 1 $$ Ainsi, comme $k$ est constante de valeur $1$, elle ne s'annule pas.
Et donc $f$ ne s'annule pas non plus, sinon elle annulerait $k$ définie par $k(x) = f(x)f(-x)$.

Soit $f$ et $g$ deux fonctions vérifiant les hypothèses du théorème, c'est à dire :
  • $f$ et $g$ définies et dérivables sur $\mathbb{R}$
  • $\color{red}{f'=f}$ et $\color{red}{g'=g}$
  • $\color{blue}{f(0)=1}$ et $\color{blue}{g(0)=1}$
Comme on a démontré que $g$ ne s'annule pas ($f$ non plus), on peut définir la fonction $h$ par $h(x) = \frac{f(x)}{g(x)}$ pour tout $x\in\mathbb{R}$.

L'objectif est de démontrer que la fonction $h$ vaut 1 et donc que $f=g$.

La fonction $k$ est dérivable sur $\mathbb{R}$ : $$ \begin{array}{clll} h'(x) &=& \frac{f'(x)g(x)-f(x) g'(x)}{g(x)^2} & \\ h'(x) &=& \frac{f(x)g(x)-f(x) g(x)}{g(x)^2} & \text{car } \color{red}{f' = f} \text{ et } \color{red}{g' = g} \\ h'(x) &=& 0& \\ \end{array} $$ Donc la fonction $h$ est constante car sa dérivée est nulle. On calcule sa valeur : $$ h(0) = \color{blue}{\frac{f(0)}{g(0)} = \frac{1}{1}} = 1 $$ Ainsi, pour tout $x\in \mathbb{R}$, $\frac{f(x)}{g(x)} = 1$, et donc $f(x)=g(x)$.

Il est important en mathématique (et ailleurs) qu'une définition soit bien fondée. C'est ce qu'on a fait en prouvant qu'il existe une unique fonction vérifiant les hypothèses du théorème. On peut maintenant entrer dans le vif du sujet... Cette fonction unique, on l'appelle la fonction exponentielle : L'unique fonction $f$ dérivable sur $\mathbb{R}$ telle que $f'=f$ et $f(0)=1$ est appelée la fonction exponentielle. On la note : $$ f(x)=exp(x) \text{ ou } f(x)=e^x $$ Ce qui au passage nous permet de découvrir une nouvelle constante mathématiqueLes constantes mathématiques sont des nombres suffisamment important dans une théorie pour avoir leur propre lettre réservée. On connaît déjà $\pi$ la constante de géométrie et $i$ l'imaginaire pur. La constante $e$ est un nombre réel irrationnel comme $\pi$. : On définit le nombre réel $e$ par $e=exp(1)=e^1$. $e\simeq 2,718$ On rappelle les propriétés de cette fonction rencontrées dans la preuve précédente :
  • $exp'=exp$ ou $[e^x]'=e^x$ (hypothèses théorème)
  • $exp(0)$ ou $[e^0]'=1$ (hypothèses théorème)
  • $e^{-x}=\frac{1}{e^{x}}$ (conclusion de la partie 1 de la preuve)
  • Soient $a,b \in \mathbb{R}$. On pose $f(x) = e^{ax+b}$, alors $f'(x) = a e^{ax+b}$
  • Soit $u$ une fonction dérivable sur $I$. On pose $f(x) = e^{u(x)}$, alors f est dérivable sur $I$ et : $$f'(x) = u'(x) e^{u(x)}$$ On peut résumer par la formule : $(e^u)' = u'e^u$
Un petit exemple pour appliquer la nouvelle formule de dérivation :

Soit $f$ définie sur $\mathbb{R}$ par $f(x)=e^{x^2}$

On applique la formule précédente avec $u=x^2$ et donc $u'=2x$ : $$ f'(x) = 2x e^{x^2} $$

Propriétés de la fonction $x\mapsto e^x$

Il faut retenir un certain nombre de règles de calculs... mais normalement, vous les connaissez déjà car ce sont les règles de calculs avec les exposants ! Nous les rappelons quand même, au cas où : Soient $a$ et $b$ deux réels, $n$ un entier :
  • $e^{0} = 1$
  • $e^{1} = e$
  • $e^{a+b} = e^a \times e^b$
  • $e^{a-b} = \frac{e^a}{e^b}$
  • $e^{n\times a} = (e^a)^n$
 Un petit peu d'entraînement... Simplifier les expressions suivantes : $e^{2x} e^{1 - 2x}$ $\frac{e^{x}}{e^{1 + x}} $ $(e^x + e^{-x})^2$ $e^{2x} - \frac{{e^{x}}^3 + e^{x}}{e^{x}}$ $$ \begin{array}{lll} && e^{2x} e^{1 - 2x}\\ &=& e^{2x + 1 - 2x}\\ &=& e^{1}\\ &=& e \end{array} $$ $$ \begin{array}{lll} &&\frac{e^{x}}{e^{1 + x}}\\ &=&e^{x- (1+x)}\\ &=&e^{x-1-x}\\ &=&e^{-1}\\ &=&\frac{1}{e}\\ \end{array} $$ $$ \begin{array}{lll} && (e^x + e^{-x})^2\\ && (e^x)^2 + 2e^x e^{-x} + (e^{-x})^2\\ && e^{2x} + 2e^{x -x} + e^{-2x}\\ && e^{2x} + 2e^{0} + e^{-2x}\\ && e^{2x} + 2\times 1 + e^{-2x}\\ && e^{2x} + e^{-2x} + 2 \end{array} $$ $$ \begin{array}{lll} && (e^x + e^{-x})^2\\ && (e^x)^2 + 2e^x e^{-x} + (e^{-x})^2\\ && e^{2x} + 2e^{x -x} + e^{-2x}\\ && e^{2x} + 2e^{0} + e^{-2x}\\ && e^{2x} + 2\times 1 + e^{-2x}\\ && e^{2x} + e^{-2x} + 2 \end{array} $$

Etude de la fonction $x\mapsto e^x$

Nous allons réaliser l'étude complète (variations, équations, limites) de la fonction exponentielle. Chaque résultat nous permet d'avancer dans notre investigation afin de connaître un peu mieux cette fonction. Nous savions déjà que la fonction exponentielle ne s'annulait pas, nous apprenons maintenant qu'elle est strictement positive : Pour tout $x \in \mathbb{R}$, $e^x \gt 0$. Nous donnons deux preuves très différentes de ce résultat : Soit $x\in\mathbb{R}$ : $$ e^x = e^{2 \times \frac{x}{2}} = (e^{\frac{x}{2}})^2 $$ et un carré est toujours positif Autre preuve : Supposons par l'absurde que $e^a \lt 0$ pour un certain réel $a$ :

On sait que :

  • La fonction $x\mapsto e^{x}$ est continue car dérivable sur $\mathbb{R}$
  • $e^0 = 1 \gt 0$
  • $e^a \lt 0$
Donc d'après le théorème des valeurs intermédiaires, la fonction s'annule au moins une fois entre $0$ et $a$. Ce qui contredit le fait que la fonction ne s'annule pas.

Et comme l'exponentielle est sa propre dérivée, naturellement : La fonction $x \mapsto e^x$ est strictement croissante sur $\mathbb{R}$ Ce résultat a pour conséquence les propriétés suivantes, très utiles pour résoudre de nouvelles équations (comme nous allons le voir juste après) : Pour tous réels $a$ et $b$ :
  • $a \lt b$ si et seulement si $e^a \lt e^b$
  • $a = b$ si et seulement si $e^a = e^b$
 Ce qui nous permet de résoudre équations et inéquations "exponentielles" comme dans l'exercice suivant : Résoudre : $e^{2x} = e^3$ $e^{-2x+6} \lt 1$ $\frac{e^{4x+1}}{e^{3x+1}} \geq e$ $e^{x}=e^{\frac{2}{x}}$ Il est possible de s'entraîner à l'aide de cet exerciseur. $$ \begin{array}{cccll} & & e^{2x} &=& e^3\\ &\Leftrightarrow& e^{2x} &=& e^3&\\ &\Leftrightarrow& 2x &=& 3& \text{car } a=b \Leftrightarrow e^a = e^b\\ &\Leftrightarrow& x &=& \frac{3}{2}\\ \end{array} $$ $$ \begin{array}{cccll} && e^{-2x+6} &\lt& 1 & \\ &\Leftrightarrow& e^{-2x+6} &\lt& e^0 & \text{car } e^0=1\\ &\Leftrightarrow&-2x+6 &\lt& 0 & \text{car } a\lt b \Leftrightarrow e^a \lt e^b\\ &\Leftrightarrow&-2x &\lt& -6 & \\ &\Leftrightarrow&x &\gt& \frac{-6}{-2} & \text{car } -2\lt 0 \\ &\Leftrightarrow&x &\gt& 3 & \text{car } -2\lt 0 \\ \end{array} $$ $$ \begin{array}{cccll} & & \frac{e^{4x+1}}{e^{3x+1}} &\geq& e &\\ &\Leftrightarrow& \frac{e^{4x+1}}{e^{3x+1}} &\geq& e^1 & \text{car } e^1=e\\ &\Leftrightarrow& e^{4x+1 - (3x+1)} &\geq& e^1 & \text{car } e^1=e\\ &\Leftrightarrow& 4x+1 - (3x+1) &\geq& 1 & \text{car } a\geq b \Leftrightarrow e^a \lt e^b \\ &\Leftrightarrow& 4x+1 - 3x-1 &\geq& 1 &\\ &\Leftrightarrow& x &\geq& 1 & \\ \end{array} $$ $$ \begin{array}{cccll} & & e ^{x}&=&e^{\frac{2}{x}}& \\ & & x&=&\frac{2}{x}& \text{car } a= b \Leftrightarrow e^a = e^b\\ & & x\times x&=&x\times \frac{2}{x}& \text{car } x\neq 0\\ & & x^2&=& 2 & \\ \end{array} $$ donc $x=-\sqrt{2}$ ou $x=\sqrt{2}$ Pour poursuivre notre investigation, nous allons calculer les limites de la fonction exponentielle.
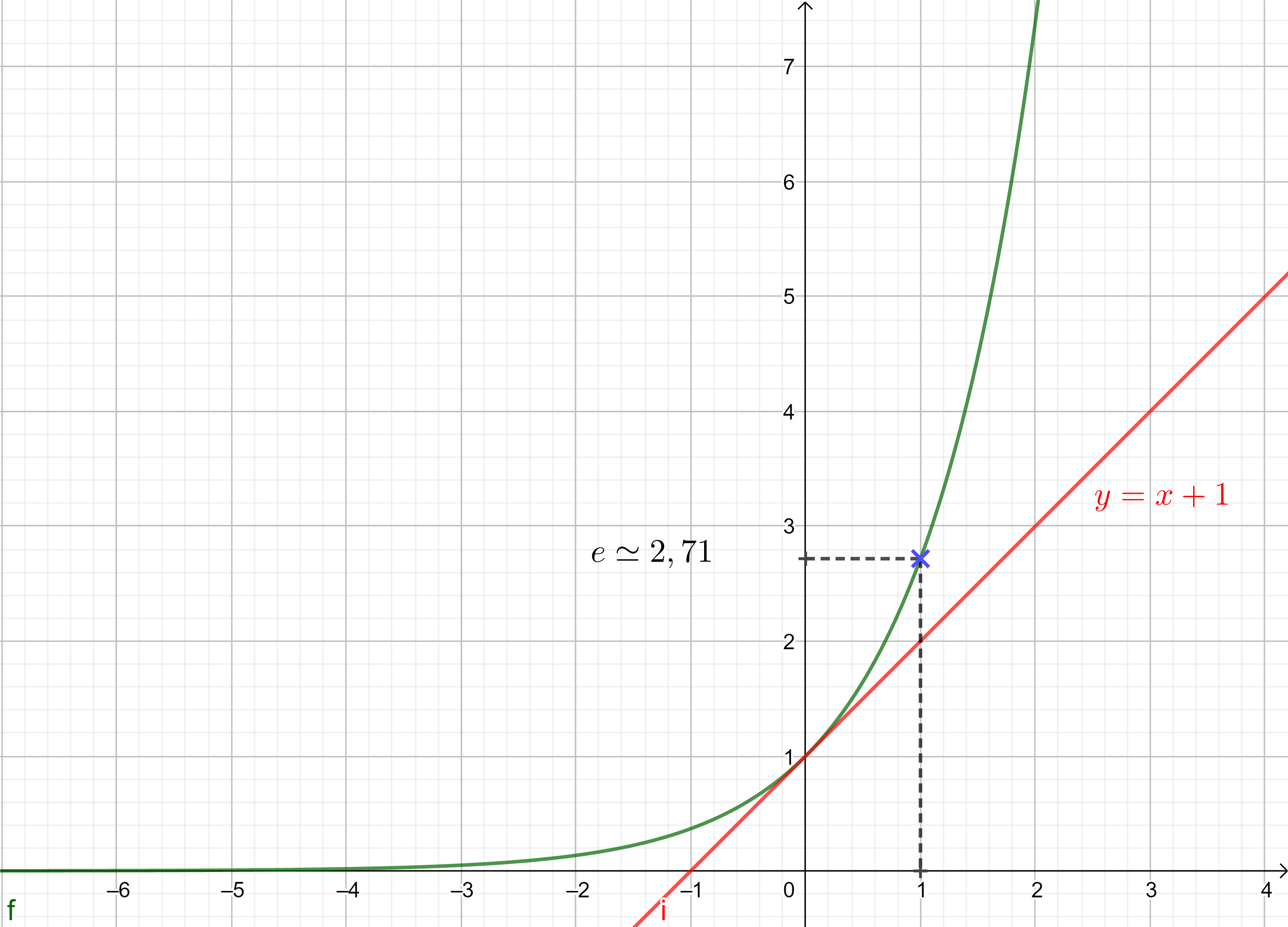
  • $\lim\limits_{x\rightarrow +\infty} e^x = +\infty$
  • $\lim\limits_{x\rightarrow -\infty} e^x = 0$

Raisonnement :

  1. En $+\infty$ : Nous allons montrer que $e^x \gt x$, puis utiliser le théorème de comparaison de limites
  2. En $-\infty$ : On va utiliser un changement de variable pour utiliser la limite en $+\infty$ et le fait que $e^{-x} = \frac{1}{e^x}$

Preuve

On commence par montrer que $e^x \gt x$ pour tout $x\in\mathbb{R}$ :

On pose $f(x) = e^x - x$ pour tout $x\in\mathbb{R}$, et on l'étudie. La fonction $f$ est dérivable : $$ f'(x)=e^x - 1 $$ On étudie le signe de la dérivée : $$ \begin{array}{lll} & & f'(x) & \gt & 0 \\ &\Leftrightarrow& e^x - 1 & \gt & 0 \\ &\Leftrightarrow& e^x & \gt & 1 \\ &\Leftrightarrow& e^x & \gt & e^0 \\ &\Leftrightarrow& x & \gt & 0 \\ \end{array} $$ On en déduit le tableau de variations de $f$ : $$ \begin{array}{c|lcccr|} x & -\infty & & 0 & & +\infty \\\\ \hline f'(x) & & - & 0 & + & \\\\ \hline f (x) & & \searrow & f(0) & \nearrow & \\\\ \hline \end{array} $$ Et comme $f(0)=e^0 - 0 = 1 \gt 0$, on en déduit que la fonction $f$ est positive et donc pour tout $x$ réel : $$ e^x \gt x $$ On utilise le théorème de comparaison des limites en $+\infty$ :

  • $ \lim\limits_{x \rightarrow +\infty} x = +\infty $
  • $ e^x \gt x$ pour tout $x\in\mathbb{R}$
Donc $\lim\limits_{x\rightarrow +\infty} e^x = +\infty$

On va utiliser le théorème de composition des limites :

On pose $g(x)=-x$ pour tout $x$ réel : $$ \begin{array}{lll} \left\{ \begin{array}{lll} \lim\limits_{x\rightarrow \color{red}{-\infty}} g(x)&=& \color{grey}{+\infty} \\ \lim\limits_{x\rightarrow \color{grey}{+\infty}} e^{-x}&=& \lim\limits_{x\rightarrow +\infty} \frac{1}{e^x} = \color{blue}{0}\\ \end{array} \right.\\ \text{Donc} \lim\limits_{x\rightarrow \color{red}{-\infty}} e^{-g(x)} = \color{blue}{0} \end{array} $$ Or, $e^{-g(x)} = e^{-(-x)} = e^x$, donc : $$ \lim\limits_{x\rightarrow -\infty} e^x = 0 $$

Toutes les conditions sont maintenant réunies pour donner le tableau de variation total et la courbe de la fonction exponentielle : En conclusion la fonction exponentielle peut être résumée par ce tableau de variations : $$ \begin{array}{c|lcccr|} x & -\infty & & 0 & 1 & & +\infty \\\\ \hline & & & & & \nearrow & \\\\ f (x) & & & 1 & e & & \\\\ & 0 & \nearrow & & & & \\\\ \hline \end{array} $$ Voici sa courbe représentative où apparaissent les variations, les limites et la tangente en $x=0$ : Le théorème suivant exprime une idée simple : "la croissance de $e^x$ l'emporte sur celle de $x$", que ça soit en $+\infty$ ou en $-\infty$ :
  • $\lim\limits_{x\rightarrow +\infty} \frac{e^x}{x} = +\infty$
  • $\lim\limits_{x\rightarrow -\infty} x e^x = 0$

Raisonnement :

  1. Pour $\lim\limits_{x\rightarrow +\infty} \frac{e^x}{x}$ : Nous allons montrer que $e^x \gt \frac{x^2}{2}$, puis utiliser le théorème de comparaison de limites
  2. Pour $\lim\limits_{x\rightarrow -\infty} x e^x$ : On va utiliser un changement de variable pour utiliser la limite en $+\infty$ et le fait que $e^{-x} = \frac{1}{e^x}$

Preuve

On commence par montrer que $e^x \gt \frac{x^2}{2}$ pour tout $x \geq 1$ :

On pose $f(x) = e^x - \frac{x^2}{2}$ pour tout $x\in\mathbb{R}$, et on l'étudie. La fonction $f$ est dérivable : $$ f'(x)=e^x - 2 \frac{x}{2} = e^x - x $$ Or, on a déjà démontré que $e^x - x \gt 1 \gt 0$ au théorème des limites la fonction exponentielle. On en déduit donc le tableau de variations de $f$ : $$ \begin{array}{c|lcccr|} x & -\infty & & 0 & & +\infty \\\\ \hline f'(x) & & & + & & \\\\ \hline f (x) & & \nearrow & 1 & \nearrow & \\\\ \hline \end{array} $$ Et comme $f(0)= 1 \gt 0$, on en déduit que la fonction $f$ est positive et donc pour tout $x \geq 1$ : $$ \begin{array}{lllll} & & e^x &\gt& \frac{x^2}{2} & & \Rightarrow & \frac{e^x}{x} & gt & \frac{x}{2} & \text{car } x\gt 0 \end{array} $$ On utilise le théorème de comparaison des limites en $+\infty$ :

  • $ \lim\limits_{x \rightarrow +\infty} \frac{x}{2} = +\infty $
  • $ \frac{e^x}{x} \gt \frac{x}{2}$ pour tout $x \gt 1 $
Donc $\lim\limits_{x\rightarrow +\infty} \frac{e^x}{x} = +\infty$

On va utiliser le théorème de composition des limites :

On pose $g(x)=-x$ pour tout $x$ réel : $$ \begin{array}{lll} \left\{ \begin{array}{lll} \lim\limits_{x\rightarrow \color{red}{-\infty}} g(x)&=& \color{grey}{+\infty} \\ \lim\limits_{x\rightarrow \color{grey}{+\infty}} x e^{-x}&=& \lim\limits_{x\rightarrow +\infty} \frac{x}{e^x} = \color{blue}{0}\\ \end{array} \right.\\ \text{Donc} \lim\limits_{x\rightarrow \color{red}{-\infty}} g(x)e^{-g(x)} = \color{blue}{0} \end{array} $$ Or, $ g(x) e^{-g(x)} = -x e^{-(-x)} = - x e^x$, donc : $$ \lim\limits_{x\rightarrow -\infty} x e^x = 0 $$

En fait, la croissance de l'exponentielle est même plus forte que n'importe quel polynôme : Pour tout $n$ entier :
  • $\lim\limits_{x\rightarrow +\infty} \frac{e^x}{x^n} = +\infty$
  • $\lim\limits_{x\rightarrow -\infty} x^n e^x = 0$
C'est tout pour aujourd'hui !