- Connaître les dérivées des fonctions cosinus et sinus
- Connaîtres les propriétés de parité et périodicité
- Connaître les représentations graphiques de ces fonctions
 Pas de panique ! On risque bien sûr de ressortir quelques formules, mais on étudiera surtout des fonctions trigonométriques (dérivées, signes, variations, limites, etc. )...
Pas de panique ! On risque bien sûr de ressortir quelques formules, mais on étudiera surtout des fonctions trigonométriques (dérivées, signes, variations, limites, etc. )...
 ... ces fonctions trigo, nous en avons déjà entendu parler, ce sont les fonctions sinus et cosinus. Elles sont liées au cercle (trigo) et permettent de représenter toutes sortes de phénomènes périodiques (et circulaires).
... ces fonctions trigo, nous en avons déjà entendu parler, ce sont les fonctions sinus et cosinus. Elles sont liées au cercle (trigo) et permettent de représenter toutes sortes de phénomènes périodiques (et circulaires).







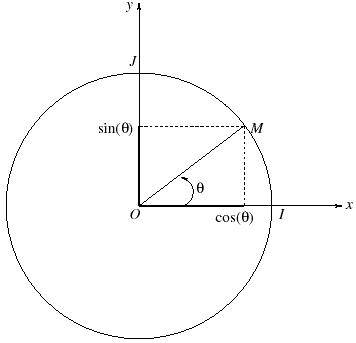 $$
M(cos(\Theta);sin(\Theta))
$$
$$
M(cos(\Theta);sin(\Theta))
$$
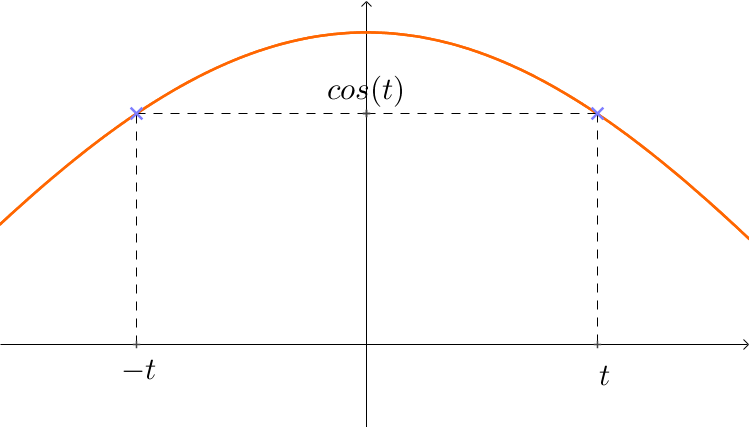
- La fonction cosinus est paire : pour tout $t\in\mathbb{R}$, $cos (-t) = cos (t)$
- La fonction sinus est impaire : pour tout $t\in\mathbb{R}$, $sin (-t) = sin (t)$
- La courbe représentative d'une fonction paire est symétrique par rapport à l'axe des ordonnées (commes la fonction carré $x^2$)
- La courbe représentative d'une fonction impaire est symétrique par rapport à l'origine du repère (commes la fonction cube $x^3$)
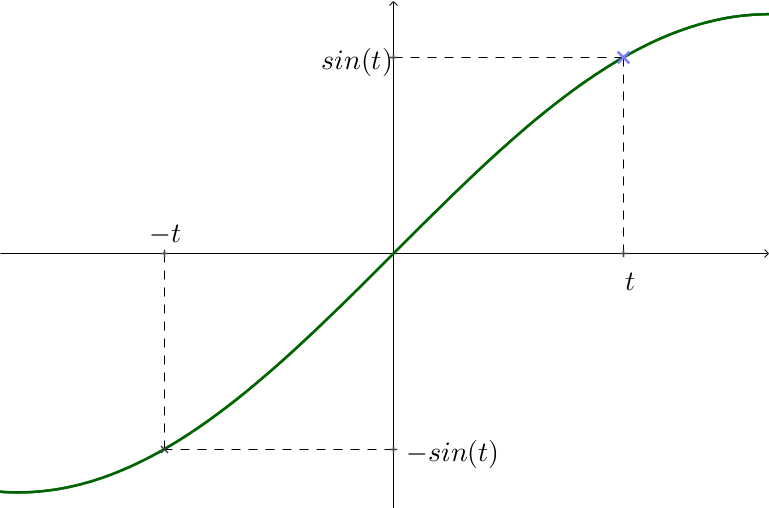
- Pour tout $t\in\mathbb{R}$, $cos (t + 2 \pi) = cos (t)$
- Pour tout $t\in\mathbb{R}$, $sin (t + 2 \pi) = sin (t)$
Une fonction périodique de période $T$ (ici $T=2 \pi$) se trace d'abord sur l'intervalle $[-\frac{T}{2};\frac{T}{2}[$ (ou parfois sur $[0;T]$).
Le reste de la courbe s'obtient par translations successives de vecteur horizontal $T \vec{i}$.
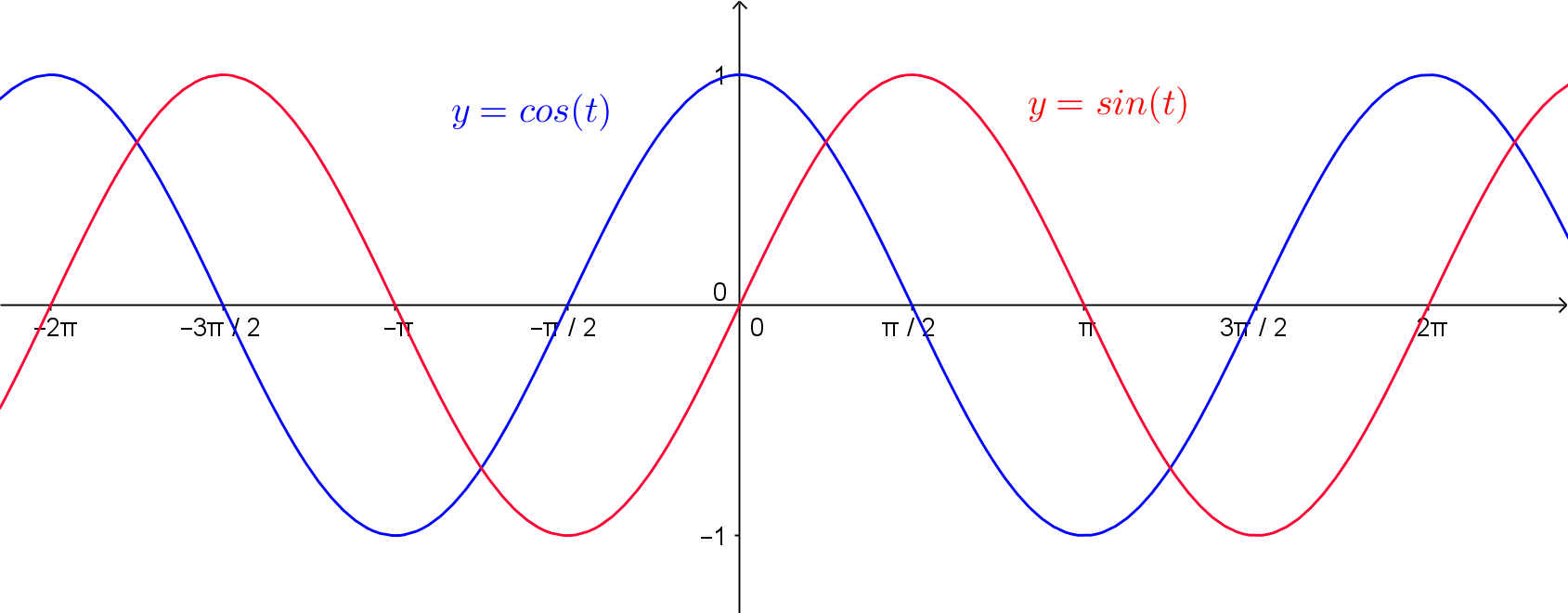
 C'était une blague... en vrai c'est beaucoup plus effrayant :
C'était une blague... en vrai c'est beaucoup plus effrayant :
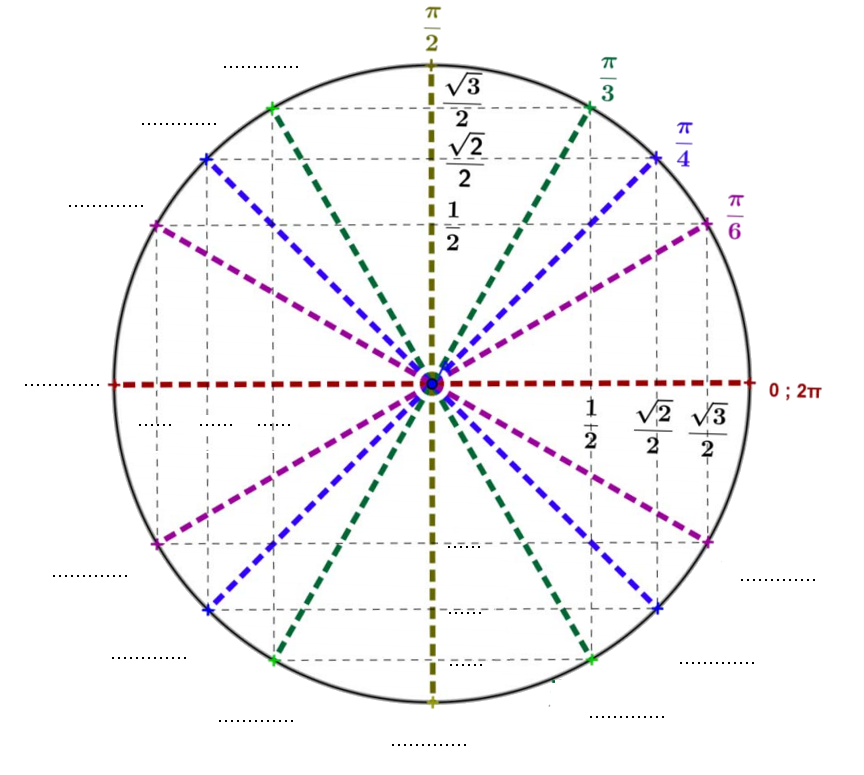
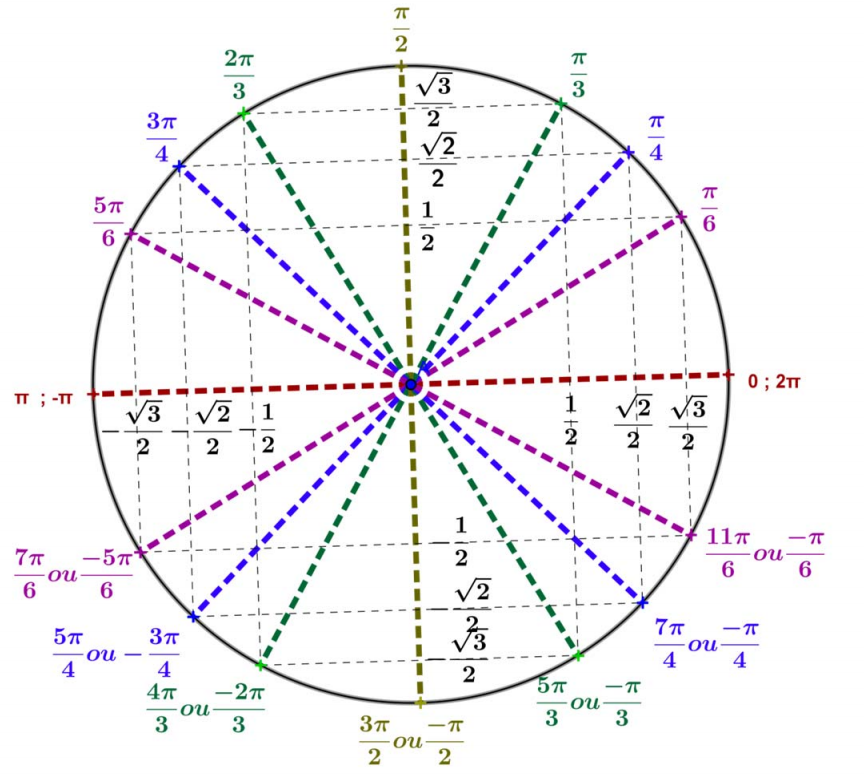
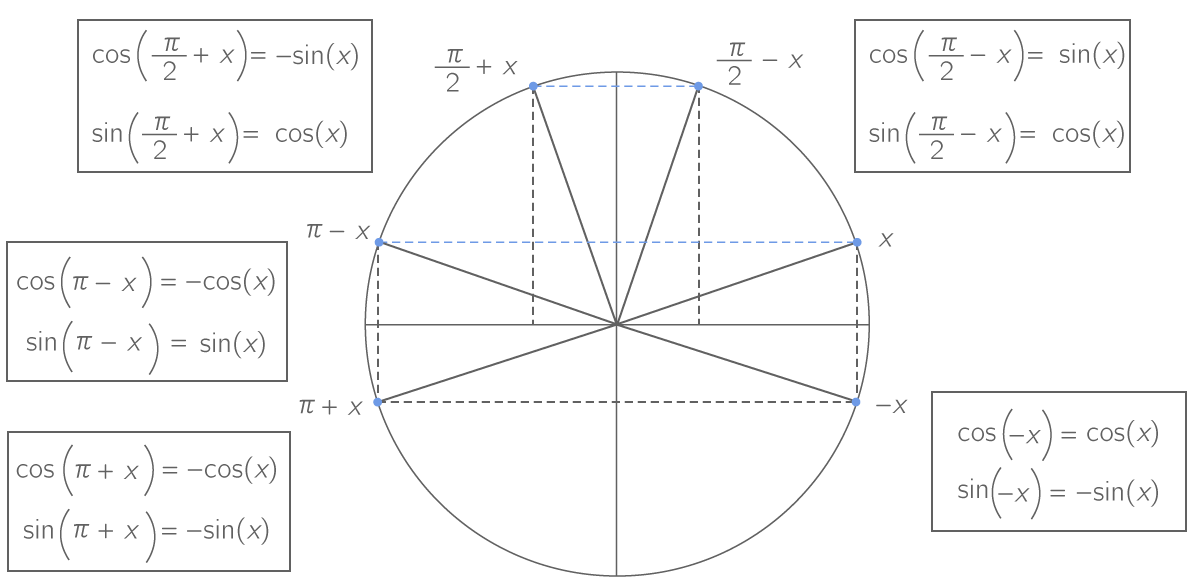 Mais pour rester (un peu) sérieux, une bonne technique est de ne retenir que le premier quart du cercle trigo et de déduire les autres par symétrie, comme on l'a déjà fait pour les valeurs remarquables.
Mais pour rester (un peu) sérieux, une bonne technique est de ne retenir que le premier quart du cercle trigo et de déduire les autres par symétrie, comme on l'a déjà fait pour les valeurs remarquables.
Etude de signe des fonctions trigo :
A l'aide du cercle trigo, on déduit le signe des fonctions sinus et cosinus :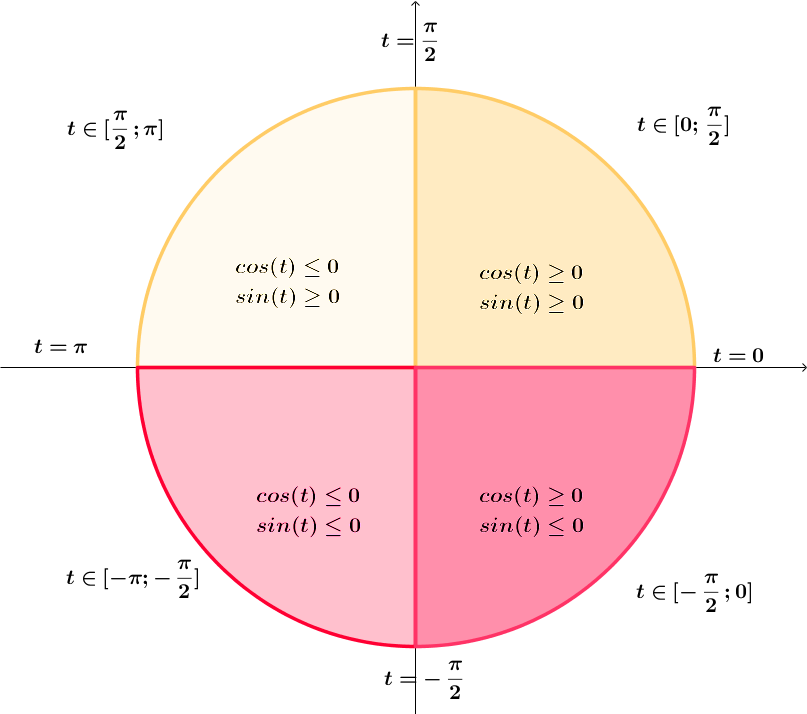
| $$ \begin{array}{c|lcccr|} t &-\pi & & \frac{-\pi}{2} & & \frac{\pi}{2} & & \pi\\\hline cos (t) & & - & 0 & + & 0 & - & \\ \hline \end{array} $$ | $$ \begin{array}{c|lcccr|} t &-\pi & & 0 & & \pi\\\hline sin (t) & & - & 1 & + & \\ \hline \end{array} $$ |
Etude du sens des variations
| $$ \begin{array}{c|lcccr|} t & -\pi & & \frac{-\pi}{2} & & \frac{\pi}{2} & & \pi \\\hline sin' (t)=-cos (t)& & - & & + & & - & \\ \hline & 0 & & & & 1 & & \\ sin (t) & & \searrow & & \nearrow & & \searrow & \\ & & & -1 & & & & 1 \\ \hline \end{array} $$ | $$ \begin{array}{c|lcccr|} t & -\pi & & 0 & & \pi \\\hline cos' (t)=sin (t) & & + & & - & \\ \hline & & & 0 & & \\ cos (t) & & \nearrow & & \searrow & \\ & -1 & & & & -1 \\ \hline \end{array} $$ |
Une forme indéterminée classique
Une application classique du calcul sur les dérivées est de résoudre la forme indéterminée suivante :Or, il s'agit exactement de la limite que l'on cherche à déterminer.
Mais comme on sait que sin'(0)=cos (0)=1, on obtient sa valeur.