Activité
Cette fiche d'activité présente plusieurs shakeparadoxes/shake qui peuvent sembler illogiques ou impossibles au premier coup d'oeil, mais qui ne résisteront pas aux outils de l'analyse mathématique. Les ifonctions affines/i nous permettrons d'expliquer chaque situation.
Le premier paradoxe devrait nous ouvrir l'appétit...

Voici une vidéo d'un paradoxe qui permettrait de faire du chocolat à l'infini :
iframe width="560" height="315" src="https://www.youtube.com/embed/yWXM65MV8lU" frameborder="0" allowfullscreen/iframe
Le but de l'exercice est de comprendre où est passé le carreau supplémentaire.
On représente la tablette de chocolat découpée dans un repère orthogonal $(O;I;J)$ où l'origine $O$ est en bas à droite, et les unités sont données par les dimensions d'un carreau.
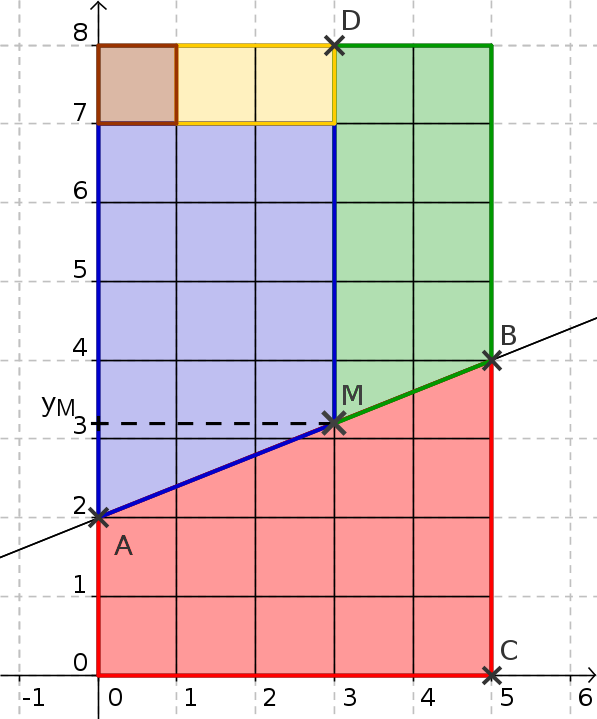
Découpage
-
-
Déterminer l'équation de la droite $AB$.
-
En déduire les coordonnées $(x_M;y_M)$ du point $M$
-
En déduire les dimensions de chacun des 5 quadrilatères découpant la tablette
Modification de la tablette
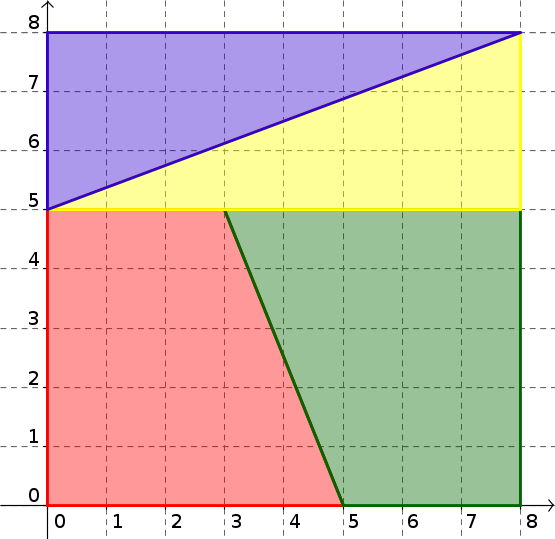
On a déplacé les morceaux découpés, et on obtient le découpage suivant avec le fameux morceau "supplémentaire" :

-
-
Quelles sont les dimensions de la nouvelle tablette ?
-
Conclure.
Le puzzle suivant a été inventé par Lewis Carrol, l'auteur de iAlice au pays des merveilles/i, qui était mathématicien. Il s'agit d'un paradoxe car il propose un découpage qui change visiblement l'aire de la figure totale...

-
-
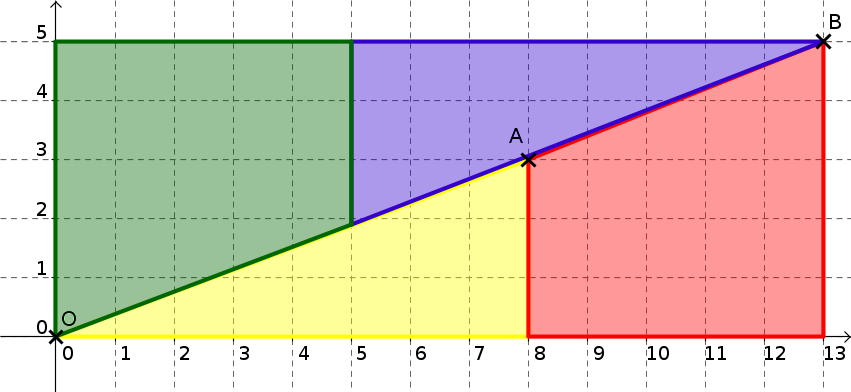
Observations
-
Calculer l'aire des deux figures et constater le paradoxe.
Explications
-
Nous allons maintenant tenter de l'expliquer à l'aide des fonctions affines :
-
Calculer l'équation de la droites $(OA)$
-
Calculer l'équation de la droite $(AB)$
-
-
Les droites $(OA)$ et $(AB)$ sont-elles parallèles, sécantes ou confondues ?
-
Que peut-on en déduire sur l'alignement des points $O$, $A$ et $B$ ?
-
Conclure.
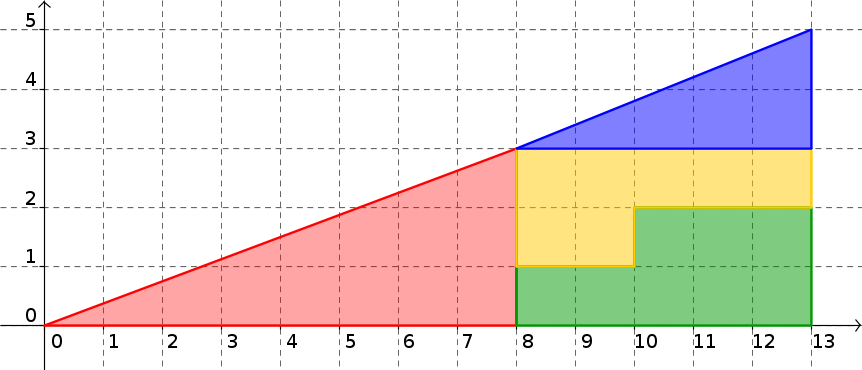
Les deux figures ci-dessous sont également un paradoxe proposé par Lewis Caroll...

Voici deux figures agencées selon les mêmes pièce :
-
-
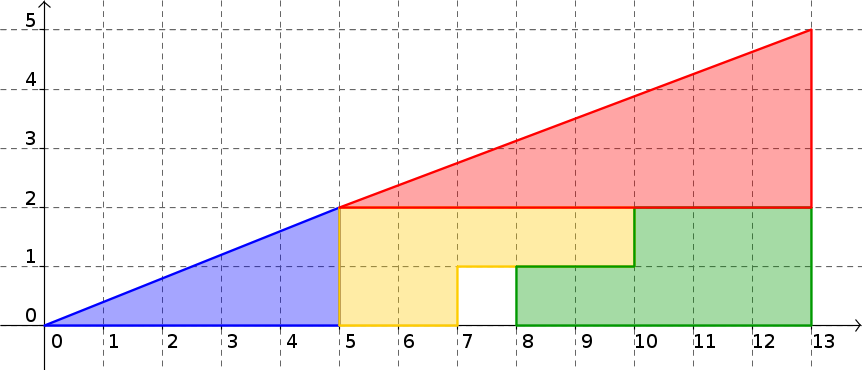
-
En comparant les deux figure, un paradoxe semble apparaître. Lequel ?
-
En étudiant l'alignement de trois points correctement choisis, expliquer ce paradoxe apparant.
>
C'est fini pour aujourd'hui !










